ΔABN=ΔCDK по катету и гипотенузе, AB=DC /противолежащие стороны прямоугольника равны/, KD=BN /как равные высоты в равных треугольниках АВС и АDC, на которые их разбивает диагональ АС/
Отсюда следует, что AN=СК.
Рассмотрим Δ АВС , в нем ВN²=(AN*NC) по свойству высоты, проведенной из вершины прямого угла на гипотенузу. Пусть AN=х; х>0, тогда NC=(9+х); 36=х*(9+х); х²+9х-36=0; По Виета х=-12, х∈∅, х=3, Значит, АС=2*х+9=2*3+9=9+6=15/см/
Площадь прямоугольника найдем как сумму двух одинаковых прямоугольных треугольников АВС и АDC. 2*(АС*ВN/2)=15*6=90/см²/
Пусть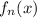 
означает 
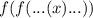, где 
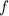применена 
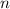раз.
Поскольку 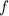многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: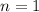 
- это то, что дано по условию.
Переход:
Пусть для некоторого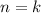 
верно; Докажем, что из этого следует справедливость утверждения и для 
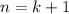; Действительно, по предположению индукции множество решений уравнения 
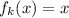совпадает с 
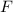; Возьмем 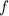от обеих частей (благодаря (*) мы можем это сделать): 
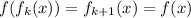; Но если сделать замену 
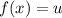, получим 
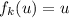; А множество решений этого уравнения лежит в 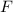; Предположим, что есть некоторый элемент 
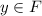, такой, что для него не найдется 
, чтобы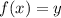 
; Тогда 
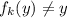, но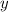 
лежит в 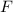, противоречие. Это завершает переход.
46-39 = 7
ответ: Витя должен отдать 7 солдатиков