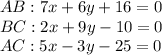
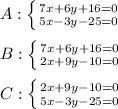
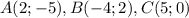
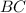 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: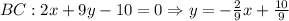
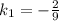
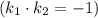 найдем
найдем 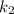 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 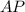 :
: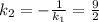
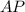 найдем по точке
найдем по точке 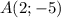 и угловому коэффициенту
и угловому коэффициенту 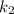 :
: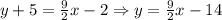
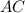 как уравнение с угловым коэффициентом:
как уравнение с угловым коэффициентом: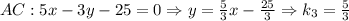
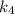 – угловой коэффициент прямой, содержащей высоту
– угловой коэффициент прямой, содержащей высоту 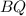 , то
, то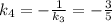
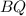 найдем по точке
найдем по точке 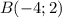 и угловому коэффициенту
и угловому коэффициенту 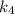 :
:
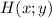 найдем, решив систему уравнений, задающих прямые
найдем, решив систему уравнений, задающих прямые 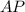 и
и 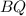 :
: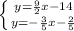
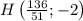
2-(нечётные)37,9