ответ: S = 6,75
Пошаговое объяснение:
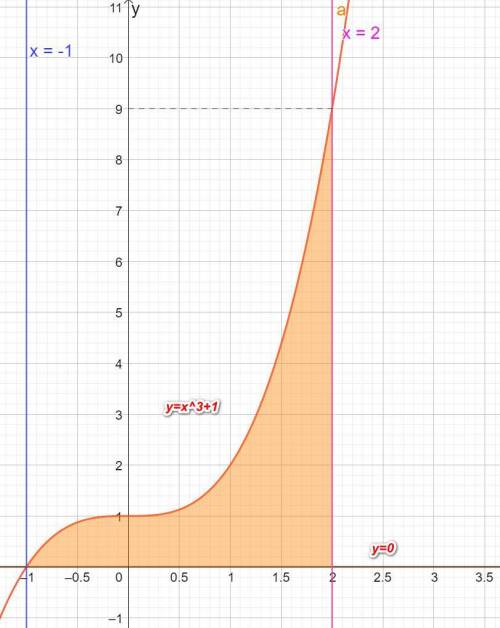
Вычислите площадь фигуры, ограниченной линиями у = х³ + 1, х = -1, х = 2 и у = 0
На координатной плоскости построим данные линии.
х = -1 и х = 2 прямые параллельные оси ординат Оу и проходящие через точки (-1;0) и (2;0) соответственно.
Прямая у = 0 лежит на оси абсцисс Ox.
у= x³+1 является кубической параболой.
График построим по точкам (-1;0), (0;1), (1;2), (2;9)
Область ограничена:
сверху кривой у= x³+1
снизу у = 0
справа х = 2
слева х =-1
Для нахождения площади найдем определенный интеграл функции x³+1 с пределами интегрирования от -1 до 2

1)22% этого числа - 440
X -100%
440 - 22% ⇔ X=440·100/22 =2000
2) 45% этого числа - 180
X -100%
180 - 45% ⇔ X=180·100/45 =400
3) 2,5% э.ч. (этого числа) -50
X -100%
50 -2,5% ⇔ X=50·100/2,5 =2000
4) 200% э.ч. 188
X -100%
188 - 200% ⇔ X=188·100/200 =94
5) 9,6% э.ч 4,8
X -100%
4,8 - 9,6% ⇔ X=4,8·100/9,6 =50
6)300% э.ч. - 6
X -100%
6 - 300% ⇔ X=6·100/300 =2