Пошаговое объяснение:
Так как надо узнать на каком месте оказалось число 995 , вычислим сумму цифр этого числа 9+9+5=23 , с такой суммой цифр это число наибольшее и последнее по порядку возрастания. За этим числом будут идти числа с суммой цифр 24 ,25,26 и последнее 27 т.е.
числа, которые имеют сумму 24 это- 699, 789, 798, 879, 888, 897, 969, 978, 987, 996;
числа, которые имеют сумму 25 это- 799, 889, 898, 979, 988, 997;
числа, которые имеют сумму 26 это- 899, 989, 998;
и последнее число имеющее сумму 27 это- 999
Получается , что за числом 995 всего 20 чисел. Всего по условию будет выписано 1000 чисел
Отсюда имеем 1000−20= 980
т.е. число 995 будет на 980-м месте
Преобразуем: 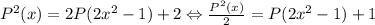 . Сделаем замену:
. Сделаем замену:  (полином имеет значение в любой точке), тогда:
(полином имеет значение в любой точке), тогда: 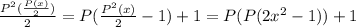 . Отсюда:
. Отсюда:  , поскольку
, поскольку  . Пусть
. Пусть  обозначает примененную
обозначает примененную  раз композицию функции
раз композицию функции  с самой собой. Аналогичным образом связана функция
с самой собой. Аналогичным образом связана функция  с функцией
с функцией  . Продолжая вышеуказанные подстановки, приходим к равенству
. Продолжая вышеуказанные подстановки, приходим к равенству  . Теперь:
. Теперь:  , поскольку
, поскольку  (здесь
(здесь 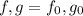 ). Но
). Но  , значит,
, значит,  , но старший коэффициент
, но старший коэффициент  положителен, откуда
положителен, откуда  . Пусть старший коэффициент
. Пусть старший коэффициент  равен
равен  . Предположим, что
. Предположим, что  . Посчитаем старший коэффициент слева:
. Посчитаем старший коэффициент слева:  , где
, где  — степень многочлена
— степень многочлена  . Старший коэффициент справа равен старшему коэффициенту
. Старший коэффициент справа равен старшему коэффициенту  и равен
и равен  . Приравниваем:
. Приравниваем:  (поскольку
(поскольку  ). В частности,
). В частности,  .
.
Заметим, что старший коэффициент  равен
равен  (в этом несложно убедиться). Тогда
(в этом несложно убедиться). Тогда  , но такого натурального
, но такого натурального  нет. Стало быть,
нет. Стало быть,  , то есть
, то есть  константа. Пусть
константа. Пусть  :
:  .
.
8/2=4 дня- будут красить 10 маляров
, т.к. между количество. раб. и объемом работ обратнопропорцион. зависимость, то 8x5=40 дней - красит один маляр