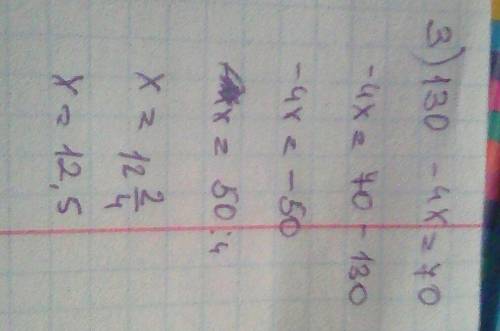
1
Пошаговое объяснение:
1) y=(x2-5·x+8)^6
((x2-5·x+8)^6)' = (12·x-30)·(x2-5·x+8)^5
Поскольку:
((x2-5·x+8)^6)' = 6·(x2-5·x+8)^(6-1)((x2-5·x+8))' = (12·x-30)·(x2-5·x+8)^5
(x2-5·x+8)' = (x2)' + (-5·x)' + (8)' = 2·x + (-5) = 2·x-5
(x2)' = 2·x2-1(x)' = 2·x
(x)' = 1
(12·x-30)·(x2-5·x+8)^5
2) здесь не уверена
y=(sin(5·x2))^3
(sin(5·x2)^3)' = 30·x·sin(5·x2)^2·cos(5·x2)
Поскольку:
(sin(5·x2)^3)' = 3·(sin(5·x2))^(3-1)((sin(5·x2)))' = 30·x·sin(5·x2)^2·cos(5·x2)
(sin(5·x2))' = (sin(5·x2))'(5·x2)' = 10·x·cos(5·x2)
(5·x2)' = 5·2·x2-1(x)' = 10·x
(x)' = 1
30·x·sin(5·x2)^2·cos(5·x2)
При вычислении были использованы следующие правила дифференцирования:
(xa)' = axa-1
(a)' = 0
(f(g(x)))' = f(x)'*g(x)'
3) на картинке решить во жизни и смерти ">
Примеры
Неравенства с модулем
|x^2 - 2x + 2| + |2x + 1| <= 5
Линейные
7x - 6 < x + 12
С квадратом
-3x^2 + 2x + 5 <= 0
Со степенью
2^x + 2^3/2^x < 9
С кубом (неравество третьей степени)
2x^3 + 7x^2 + 7x + 2 < 0
С кубическим корнем
cbrt(5x + 1) - cbrt(5x - 12) >= 1
С натуральным логарифмом
(ln(8x^2 + 24x - 16) + ln(x^4 + 6x^3 + 9x^2))/(x^2 + 3x - 10) >= 0
Иррациональные с квадратным корнем
sqrt(x - 2) + sqrt(x - 5) <= sqrt(x- 3)
Показательные неравенства
8^x + 18^x > 2*27^x
Логарифмические неравенства
log(((7 - x)/(x + 1))^2)/log(x + 8) <= 1 - log((x + 1)/(x - 7))/log(x + 8)
Тригонометрические
tg(x - pi/3) >= -sqrt(3)
Квадратное неравенство
25x^2 - 30x + 9 > 0
С четвёртой степенью
(x - 6)^4*(x - 4)^3*(x + 6)/(x - 7) < 0
С дробью
2x^2 - 15x + 35 - 30/x + 8/x^2 >= 0
Решение с целыми числами
(4x^2 - 3x - 1)/(2x^2 + 3x + 1) > 0
Пошаговое объяснение:
у=4
проверка - 33*4=132
2.2х=15+13
2х=28
х=28:2
х=14
проверка 2*14=15+13
3. 130-4х=70
4х=130-70
4х=60
х=60:4
х=15
4. 9у-89=55
9у=55+89
9у=144
у=144:9
у=16
проверка - 9*16+89=55