Дано:
тр АВС - р/б
АС - основание
ВН - высота
АВ : АС = 5 : 8
ВН = 7,2 см
Р(АВС) периметр - ?
Пусть х см- в одной части, тогда каждая из боковых сторон 5х см, а основание 8х см. ВН - высота и => медиана р/б тр АВС по св-ву р/б тр, значит АН= НС = 4х см. ПО т Пифагора к тр ВНС составляем уравнение:
(4х)²+ 7,2 ² = (5х)²
16х² + 51,84 = 25х²
51,84 = 9х²
х² = 51,84 : 9
х² = 5,76
х(1) = 2,4 (см) в одной части
х(2) = -2,4 - не подходит под условие задачи, длина величина >0
2) 2,4 * 5 = 12 с м - каждая из двух равных боковых сторон
3) 2,4 * 8 = 19,2 см - основание р/б треугольника
4) 12 * 2 + 19,2 = 43,2 см - периметр данного треугольника
Пошаговое объяснение:
здесь все просто. нарисую на первом примере, остальные по образу и подобию
1.
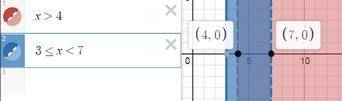
x > 4
3 ≤ x < 7
откладываем на числовой оси точки 4, 3 и 7
отмечаем промежутки, соответствующие неравенствам. где промежутки пересекутся - там и решение
у нас они пересеклись 4 < x < 7
и надо не упустить из виду, гду строгое неравенство, а где нестрого
2.
здесь решения нет (множества решений не пересекаются) т.к. в первом неравенстве 6 входит в решение, а во втором неравенство строгое - 6 не входит
3. решение 8 < x ≤ 9
4. решения не пересекаются т.к. в одном х < 12, а в другом х > 31