1 19/90.
х < 10.
Пошаговое объяснение:
5/16•(x - 5/18) = 7/24
Умножим обе части равенства на 48, получим
48•5/16•(x - 5/18) = 48•7/24
3•5 •(x - 5/18) = 2•7
15•(х - 5/18) = 14
х - 5/18 = 14 : 15
х - 5/18 = 14/15
х = 5/18 + 14/15
х = 25/90 + 84/90
х = 109/90
х = 1 19/90
Проверка:
5/16•(109/90 - 5/18) = 7/24
5/16•(109/90 - 25/90) = 7/24
5/16•84/90 = 7/24
(5•84)/(16•90) = 7/24
(1•21 )/ (4•18 ) = 7/24
(1•7)/(4•6) = 7/24
7/24 = 7/24 - верно.
Предположу, что в условии были даны некоторые неравенства. В опубликованном задании их нет. Привожу пример своего неравенства:
х < 10.
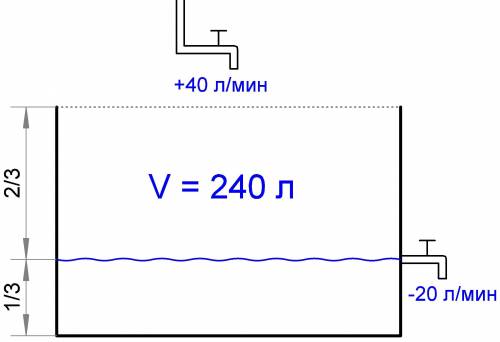
V = 240 л (объём бассейна)
v₁ = 40 л/мин (скорость истечения воды из верхнего крана)
v₂ = 20 л/мин (скорость истечения воды из нижнего крана)
1/3 от высоты бассейна (высота расположения нижнего крана)
Схема всего этого- смотри картинку внизу.
Получается, нижняя часть бассейна будет наполняться со скоростью:
v₁ = 40 л/мин (ведь из нижнего крана ещё не будет выливаться вода).
А верхняя часть бассейна будет наполняться со скоростью:
v₁ - v₂ = 40 - 20 = 20 л/мин (разность скоростей наполнения и опустошения бассейна из верхнего и нижнего кранов соответственно)
Объём нижней части бассейна равен:
V₁ = 1/3 * V = 1/3 * 240 = 80 л
Объём верхней части бассейна равен:
V₂ = V - V₁ = 240 - 80 = 160 л
Время наполнения нижней части бассейна равно:
t₁ = V₁ / v₁ = 80 / 40 = 2 мин
Время наполнения верхней части бассейна равно:
t₂ = V₂ / (v₁ - v₂) = 160 / 20 = 8 мин
Время наполнения всего бассейна равно:
t = t₁ + t₂ = 2 + 8 = 10 мин
Можно было конечно это всё подставить сразу в один общий расчёт времени, упростить и посчитав получить то же самое:
2)95-30-23=42