.
Пусть х км - весь путь мотоциклиста, тогда 0,4х км - он проехал сначала, 0,3 · (х - 0,4х) = 0,3 · 0,6х = 0,18 км - он проехал затем. После этого ему осталось проехать 105 км. Уравнение:
х - (0,4х + 0,18х) = 105
х - 0,58х = 105
0,42х = 105
х = 105 : 0,42
х = 250
- - - - - - - - - -
.
Весь путь примем за единицу (целое).
1) 40% = 40/100 = 2/5
1 - 2/5 = 5/5 - 2/5 = 3/5 - оставшаяся часть пути;
2) 30% = 30/100 = 3/10
3/5 · 3/10 = 9/50 - проехал затем;
3) 3/5 - 9/50 = 30/50 - 9/50 = 21/50 - оставшаяся часть пути, равная 105 км;
4) 105 : 21/50 = 105 · 50/21 = 5 · 50 = 250 км - весь путь.
ответ: 250 км.
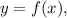где 
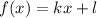, если известно, что график этой функции пересекается с графиком функции 
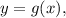где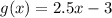 
в точке 
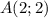, если 
.
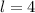, тогда как все прочие величины в выражении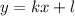 
нам известны. В задаче нам даны и величина 
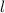, и координаты 
и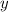 
, остается найти только неизвестную величину . и 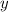? Все очень просто: в условии сказано, что график искомой нами функции пересекает график другой функции в какой-то точке 
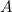. Это означает, что точка 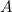принадлежит графикам обеих функций. И координаты этой точки можно подставить в выражение, задающее обе функции, и это выражение не потеряет смысла. Я докажу вам это. Возьмем известную из задания функцию 
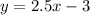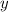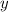и вместо переменных и подставим координаты и точки 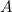. Наше выражение не потеряет смысла (то есть равенство сохранится), так как точка 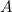принадлежит графику этой функции (иными словами она задается этим самым уравнением). Проделаем это:
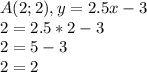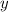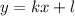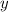. Итак, мы видим, что мои слова правдивы. Этот метод действительно работает. и в выражении подставим координаты и точки 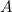, так как она принадлежит графику этой функции (что следует из условия):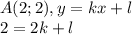
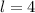и решим теперь данное уравнение:
. 
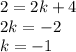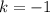, в задании же просят указать выражение, задающее нашу функцию, а оно имеет вид: 
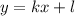, подставим теперь вместо и 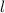их значения и получим ответ: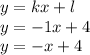
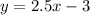. На том же графике отметим точку 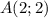. И, наконец, определим, что график вида 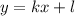— прямая, где 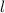— координата 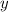точки пересечения графика с осью 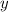. То есть, иначе говоря, наш искомый график будет проходить через точки: 
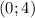(так как 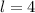из условия) и 
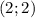(из условия следует, что такая точка графику принадлежит, значит график через нее проходит). Построим график через две данные точки. Убедимся, что данный график соответствует графику функции 
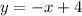(убывает, проходит через точки (-1;1), (0;0), (1;-1) при параллельном переносе 
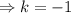, а также проходит через точку (0;4) 
). Итак, задача решена двумя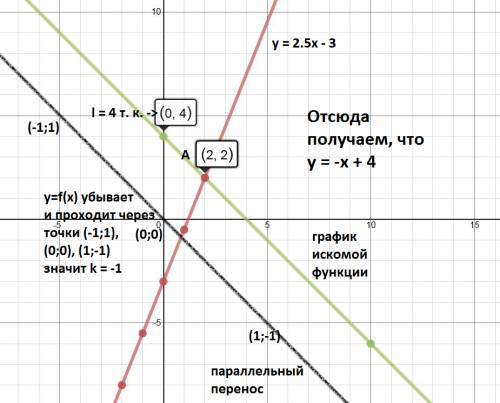 
15*7＝105кг привезли
ответ 105 кг