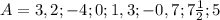(к сожалению, скобки не отображаются)
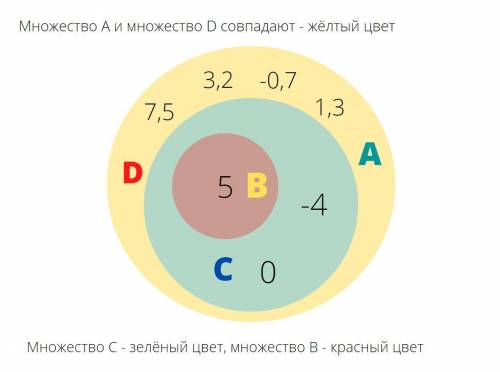
Натуральные числа (N) - те целые числа, что мы используем при счёте, не включая 0. Т.е. N={1, 2, 3, 4, 5, 6...} Выпишем такие элементы из множества А в подмножество В.
В={5}
Записывается это так: В⊂А (В включено в А, или В - часть множества А, В - подмножество множества А)
Целые числа (Z) - это множество значений координатной прямой, которые имеют вид a,(0), т.е. все натуральные числа, нуль и все отрицательные числа. Выпишем такие элементы из множества А в подмножество С.
С={-4; 0; 5}
Запишем, как С⊂А (С включено в А, или С - часть множества А, С - подмножество множества А)
Рациональные числа (Q) - это подмножество множества действительных чисел, которые можно записать в виде дроби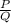 
. Иными словами, все приведённые в множестве А значения входят в множество рациональных чисел. Значит, множество А полностью соответствует множеству D.
Диаграмму представлю в прикрепе...
Чтобы сумма 100а + 10b + 5 делилась на 2/на 5/на 10 необходимо, чтобы каждое из слагаемых делилось на 2/на 5/ на 10.
Слагаемое 100а делится на каждое из чисел 2, 5 и 10. Аналогично и для 10b
Число 5 делится на 5, но не делится на 2 и 10.
Делаем вывод: данная сумма на 2 не делится, на 5 - делится, на 10 - не делится.