Задача легко решается с кругов Эйлера. Жаль, что возможности Знаний.сом не позволяют рисовать. Попробую обяснить на пальцах. У нас есть три круга, которые состоят из ребят посетивших кино, театр и цирк. Эти круги пересекаются все три - это кто был в трех местах или попарно - те, кто был в двух местах.
Сложим количество ребят побывавших в цирке, кино и театре 11+25+17=53
Так как некоторые из них побывали в двух местах, то, чтобы исключить двойной подсчет мы их из обшей суммы вычтем
53-10-4-6=33
В классе всего 36 учеников, но так как двое вообще никуда не ходили, то 36-2=34 - остается 34.
Следовательно 34-33=1. Получается один человек был во всех трех местах (кино, цирк, театр).
Проверим это правило посчитав определитель второй степени:
![[\begin{array}{cc}1&2\\4&5\end{array}]\right] = 1*5 - 2*4 = -3](/tpl/images/0150/1870/c0c97.png)
Поменяем столбцы местами:
![[\begin{array}{cc}2&1\\5&4\end{array}]\right] = 2*4 - 1*5 = 3](/tpl/images/0150/1870/aa59c.png)
Если брать некоторые абстрактные значения:
![[\begin{array}{cc}a_1&a_2\\a_3&a_4\end{array}]\right]= a_1*a_4 - a_2*a_3](/tpl/images/0150/1870/72ec5.png)
Пусть 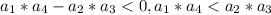
Поменяем столбцы местами:
![[\begin{array}{cc}a_2&a_1\\a_4&a_3\end{array}]\right] = a_2*a_3 - a_1*a_4 0](/tpl/images/0150/1870/45e70.png)
Далее можно было бы рассмотреть определитель n*n, но мне кажется, что и эта демонастрация будет весомым подкреплением моего заверения: что при перестановке столбцов знак определителя меняется на противоположный.
Во-первых, очень часто в системе уравнений вообще невозможно посчитать определитель, так как матрица отвечающая системе оказывается не квадратной.
А во-вторых, разумеется, определитель системы поменяет знак, если системе будет отвечать квадратная матрица и вы переставите столбцы.
Главное не путать матрицу элементов и определитель этой матрицы, это разные сущности!
Когда вы переставляете столбцы - вы меняете определитель, а система остается эквивалентной (когда перестановка осуществляется в пределах левой части, или в пределах правой. При переносе столбцов из левой в праву, или из правой в левую, надо домножать столбец на -1).
а)
54a^8b^5 - 42a^5b^3 - 24a^4b^7 = 6a^4b^3 * (9a^4b^2 - 7a - 4b^4),
2)
x^2(x-3)+2x(3-x)^2=0.
x³ - 3x² + 2x(9-6x+x²) = 0.
x³ - 3x² + 18x - 12x² + 2x³ = 0.
3x³ - 15x² + 18x = 0.
х*(3x² - 15х + 18) = 0,
х1 = 0,
3x² - 15х + 18 = 0,
Д = (-15)² - 4*3*18 = 225 - 216 = 9,
х2 = (15+3)/2*3 = 18/6 = 3,
х3 = (15-3)/2*3 = 12/6 = 2