Алгоритм исследования с второй производной на максимум и минимум включает следующие этапы: 1)нахождение первой производной заданной функции - f′(x); 2) нахождение критических точек (f′(x)=0 или не существует); 3)нахождение второй производной заданной функции - f″(x); 4)исследование знака f″(x) в критической точке; 5)определение характера критической точки; 6)вычисление значения f(x) при каждом критическом значении переменной.
Все возможные варианты, которые могут получиться в результате исследования, можно свести в таблицу (прилагается в файле)
Пример. Исследовать заданную функцию на минимум и максимум: y=12x³+4.
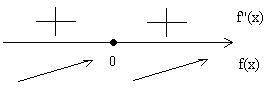
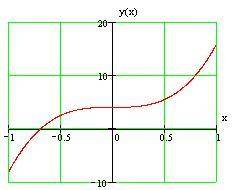
Решение: Найдем первую производную заданной функции: y′=(12x³+4)′=36x². Найдем критические точки: y′(x)=0; 36x²=0; ⇒x=0. Найдем вторую производную заданной функции: y″=(36x²)′=72x. Исследуем знак f″(x) в критической точке: y″(0)=72⋅0=0 Так как вторая производная заданной функции обращается в ноль в критической точке, то мы не можем определить характер критической точки с ее Для определения характера критической точки воспользуемся первой производной. Исследуем знак f′(x) с числовой прямой: Рисунок 7. Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума График заданной функции приведен на рис.8.
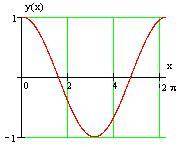
Пример 2.Исследовать заданную функцию на минимум и максимум: y=cosx. Решение: Поскольку заданная функция является периодической с периодом 2π, то можно ограничиться исследованием функции на отрезке [0;2π]. Найдем первую производную заданной функции: y′=(cosx)′=−sinx. Найдем критические точки: y′(x)=0;−sinx=0 x1=0,x2=π,x3=2π. Найдём вторую производную заданной функции: y″=(−sinx)′=−cosx. Исследуем знак f″(x) в критических точках: y''(0)=-cos 0=-1; y''(2π )=-1 Следовательно, в точках x1=0,x3=2π имеем максимум данной функции, а в точке x2=π - минимум данной функции. Вычислим значения заданной функции f(x) при каждом критическом значении переменной: y(0)=cos0=1;y(π)=cosπ=−1;y(2π)=cos2π=1 График заданной функции приведен на рис. Рисунок 9.

1)3 стула - 420 рублей 2 кресла - 560 рублей
1 стул - х рублей 1 кресло - х рублей
1)420:3=140 рублей-стоимость одного стула
2)560:2=280 рублей- стоимость одного кресла
3)280-140=140 рублей- на столько рублей кресло дороже стула
4)280:140=2-во столько раз стул дешевле кресла
2) 1)Для начала найдём периметр прямоугольника:
P=(2+6)×2=16см
2)Мы знаем формулу периметра квадрата:периметр квадрата равен 4×длину стороны квадрата
Отсюда мы можем найти сторону квадрата :
P:4=16:4=4см
Теперь нужно начертить квадрат со сторонами по 4 см.
3)S прямоугольника=6×2=12 см^2
S квадрата=4×4=16см^2
Пошаговое объяснение:
x^2 + xy + y + y^2 + xy + x = 1 + 5
(x^2 + 2xy + y^2) + (x + y) - 6 = 0
(x + y)^2 + (x + y) - 6 = 0
Получаем квадратное уравнение относительно t = x + y:
t^2 + t - 6 = 0
По теореме Виета сумма корней равна -1, произведение -6. Угадываем корни: t = -3 или t = 2.
1) t = -3
x + y = -3 [*]
Рассматриваем первое уравнение:
x^2 + xy + y = 1
x(x + y) + y = 1
-3x + y = 1
Вычитаем из уравнения [*] получившееся уравнение.
x + y + 3x - y = -3 - 1
4x = -4
x = -1
y = -3 - x = -3 + 1 = -2.
2) Аналогично с t = 2.
x + y = 2
2x + y = 1
x = -1
y = 3
ответ. (-1, -2), (-1, 3).