Ниже читай
Пошаговое объяснение:
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида.
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.
Существует ряд обобщений данной теоремы — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется
Пошаговое объяснение:
4.71
2x + Iax-5I = 0
запишем в виде Iax-5I = -2x
теперь получим первое и главное условие для решения х<0
и вот раскроем модуль
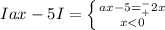
при любом раскладе 5/(а±2) должно быть <0, т.е при а> 2 решений нет
теперь рассмотрим первую строчку
ax-5 = 2x ⇒ х = 5/(а-2), при этом x<0, значит а-2<0, a<2
это мы нашли один интервал
теперь
ax-5 = 2x ⇒ х = 5/а+2, при этом x<0, значит а+2<0, a < -2
и теперь еще условие а≠ 2, т.к. знаменатель не может быть равен 0, т.е при а = 0 решений нет
ну вот, в общем-то и всё
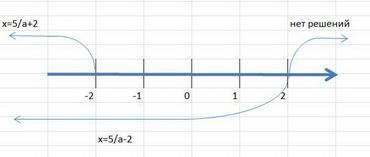
теперь нанесем все точки а и значения х на числовую ось и получим решение
a < -2 х = 5/а±2
-2 ≤a <2 х = 5/(а-2)
a ≥ 2 нет решения
(не совсем сходится с ответом, но в ответе есть ошибка. при a = -2
х не может быть равен 5/а+2, т.к. знаменатель будет 0
если k=2,34 то 4,5+18,57+k=4,5+18,57+2,34=25,41
2)b+3,71+15,2
если b=3,045 то b+3,71+15,2=3,045+3,71+15,2=21,955