Пошаговое объяснение:
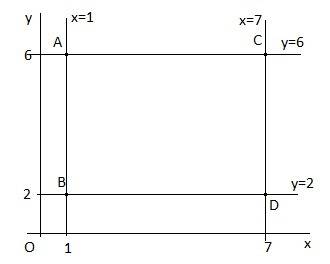
Отметим точки A, B и C на координатной плоскости. У точек A и B совпадают абсциссы точек, соединяем их прямой x = 1.
У точек A и C совпадают ординаты точек, соединяем их прямой y = 6.
Через точку B с ординатой 2 проводим прямую y = 2 параллельную прямой y = 6 (противоположной стороне прямоугольника).
Через точку C с абсциссой 7 проводим прямую x = 7 параллельную прямой x = 1 (противоположной стороне прямоугольника).
Проведенные через точки B и C прямые пересекутся в точке D(7; 2), которая и будет 4 вершиной прямоугольника ABCD.
x = (-π)/24 - πk/2
Пошаговое объяснение:
cos^2(2x - π/6) - cos^2(2x + π/6) = sqrt(3)/4;
(cos 2x * cos π/6 + sin 2x * sin π/6)^2 - (cos 2x * cos π/6 - sin 2x * sin π/6)^2 = sqrt(3)/4;
cos π/6 = sqrt(3)/2; sin π/6 = 1/2;
Умножаем сразу обе части сразу на 4
(cos 2x * sqrt(3) + sin 2x)^2 - (cos 2x * sqrt(3) - sin 2x)^2 = sqrt(3);
Используя разность квадратов, получаем:
2sqrt(3) * cos 2x * (-2) * sin 2x = sqrt(3);
2sin 2x * cos 2x = (-1/2);
sin 4x = (-1/2);
Вносим знак, получаем
sin (-4x) = sin (π/6 + 2πk);
-4x = π/6 + 2πk;
x = (-π)/24 - πk/2
2) 45:5 = 9(мин) - на повторение пройденного материала
3) 45:9 = 5(мин)
ответ: На решение задачи ученики потратили 15 минут, на повторение пройденного материала - 9 минут , на решение уравнения - 5 минут .