36 карт 4 туза, 32 не туза
а) первый туз 4/36
второй туз 3/35
третий не туз 32/34
вероятность P(т, т, н) = 3*4*32 / (34*35*36) = 16 / 1785
так как всего существует три варианта расположения "не туза"
ттн, тнт, нтт
общая вероятность P(2т) = 3 * 16/1785 = 0,027
ответ 2,7%
б) вероятность. что хотя бы одна - туз проще вычислить из вероятности события "ни одного туза"
P(3н) = 32/36 * 31/35 * 30/34 = 0,695
откуда искомая вероятность = 1 - 0,695 = 0,305
ответ: 30,5%
Пошаговое объяснение:
В трёх питомниках было 1450 саженцев. В первом и во втором питомниках на 20 саженцев больше, чем в третьем. Сколько саженцев в каждом питомнике?
Краткая запись задачи:Поскольку в первом и во втором питомниках количество саженцев совпадает, то мы можем взять количество саженцев в обоих питомниках за х. Так как в первом и во втором питомниках на 20 саженцев больше, чем в третьем, то соответственно в третьем питомнике на 20 саженцев меньше, поэтому в третьем питомнике (х - 20) (саженцев).
Алгебраическое решение задачи:1 Этап. Составление математической модели:
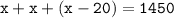
2 Этап. Работа с математической моделью:
Раскроем скобки и упростим уравнение:
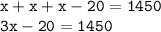
Перенесём константу в правую часть уравнения, сменив её знак и вычислим всё, что теперь будет возможно:
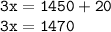
Чтобы найти неизвестный втрой множитель, необходимо произведение разделить на известный первый множитель:
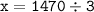
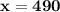(саженцев) - было и в первом, и во втором питомниках. (внимание, это не сумма саженцев первого и второго питомниках)
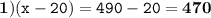(саженцев) - было в третьем питомнике.
по 490 саженцев в первом и втором питомниках, 470 саженцев в третьем питомнике.
2)5 * 7/15 = 1* 7/3 = 7/3 = 2 1/3