☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡
Производная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆♡☆
Один из это использование обычного квадратного листа бумаги. Углы 90°. Если сложит по диагонали, получаем 45°. И так далее.
Другой это с обычного клетчатого листа тетрадки.
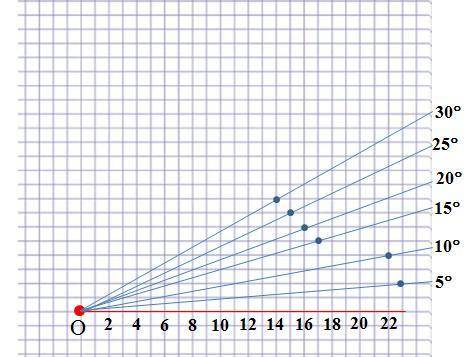
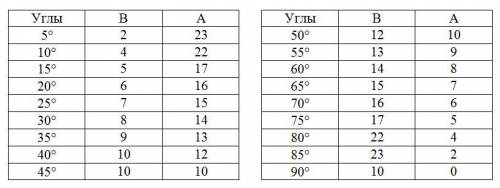
Сначала определим начальную точку О и проведём горизонтальную прямую (на рисунке цвет красный). Потом посчитаем вправо А клеток и вверх В и отмечаем точку С (на рисунке цвет синий). Проведём луч с началом в точке О и проходящий через точку С. В зависимости значений А и В получаем нужные углы (см. рис. таблицы).
Остальные углы можно получить симметричным отражением.
68м4см=6804см
1м2<10000m2
1дм2<110cм2