Пошаговое объяснение:
Квадрат гипотенузы равен сумме квадратов катетов
гипотенуза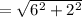 
= 
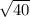
прямоугольные треугольники все равны, значит и гипотенузы их одинаковые. У закрашенной фигуры все стороны равны - это квадрат.
Площадь квадрата равна квадрату длины его стороны.
S = 
= 40 см²
Или второй
можно найти площадь прямоугольных треугольников
S = (6*2) : 2 = 6 см²
Треугольники все одинаковые и их 4
6 * 4 = 24 см² - площадь всех 4 треугольников
Теперь найти площадь большого квадрата
6 + 2 = 8 см - сторона квадрата
8 * 8 = 64 см² - площадь большого квадрата
64 см² - 24 см² = 40 см² - площадь закрашенной фигуры
Решите уравнение.
- - - - - - - - -
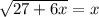
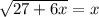
Возведём обе части уравнения в квадрат, чтобы избавиться от знака корня в левой части.
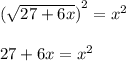
Перенесём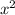 
в левую часть уравнения с противоположным знаком.
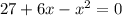
Меняем слагаемые в левой части местами.
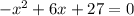
Домножаем обе части уравнения на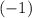 
.
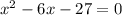
Вычисляем дискриминант.
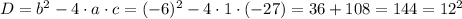
Находим корни уравнения.
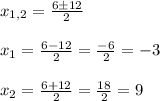
Получили, что у уравнения 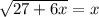есть 2 корня. Но не стоит спешить. Давайте попробуем подставить значения 
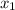и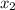 
в уравнение, и проверим, подходят ли корни.
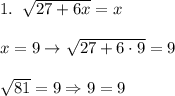
Верно! 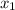подходит.
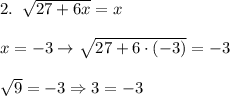
ЛОЖЬ! Этот корень не подходит. Он посторонний. Значит уравнение 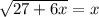имеет 1 корень. Он равен 9.
ОТВЕТ: 9.
