1) 23 и 25.
2) 7 и 24.
Пошаговое объяснение:
1) Пусть первое нечетное число равно 
, тогда следующее за ним нечетное число равно 
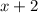. Произведение этих двух чисел равно 575. Составим уравнение.
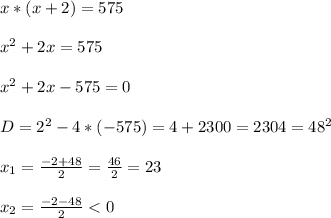
Значит первое число равно 23.
Второе число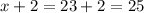 
Проверка: 23·25=575
ответ: 23 и 25.
2) Диагональ делит прямоугольник на два равных прямоугольных треугольника (см. рисунок). В получившемся прямоугольном треугольнике диагональ является гипотенузой, а стороны прямоугольника катетами.
Пусть один катет равен , тогда второй катет равен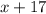 
. Гипотенуза равна 25.
По теореме Пифагора:
Ширина прямоугольника равна 7 см.
Длина прямоугольника равна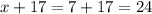 
(см)
ответ: 7 см, 24 см.
Даны координаты вершин пирамиды:
A1(4; 7; 8), A2(-1; 3; 0) , A3(2; 4; 9) , A4(1; 8; 9).
Находим:
1. Длину ребра А1А2.
Вектор А1А2 = (-1-4; 3-7; 0-8) = (-5; -4; -8).
|A1A2| = √((-5²) + (-4)² + (-8)²) = √(25 + 16 + 64) = √ 105.
2. Угол между ребрами А1А2 и А1А4.
Вектор А1А2 = (-5; -4; -8), |A1A2| = √ 105 (см.п.1).
Находим вектор А1А4 = (1-4; 8-7; 9-8) = (-3; 1; 1) и его модуль:
|A1A4| = √(9 + 1 + 1) = √ 11.
cos (A1A2_A1A4) = (-5)*(-3)+(-4)*1+(-8)*1)/(√ 105*√ 11) = 3/√ 1155 ≈ 3/33,98529.
Угол равен 0,088273 радиан или 1,4824078 градуса.
3. Площадь грани А1А2А3.
Вектор А1А2 = (-5; -4; -8) (см.п.1).
Находим вектор А1А3 = A3(2,4,9) - A1(4,7,8) = (-2; -3; 1).
Площадь равна половине модуля векторного произведения А1А2 на А1А3.
i j k| i j
-5 -4 -8| -5 -4
-2 -3 1| -2 -3 = -4i + 16j + 15k + 5j - 24i - 8k =
= -28i + 21j + 7k = (-28; 21; 7).
S = (1/2)√((-28)² + 21² + 7²) = (1/2)√(784 + 441 + 49) = (1/2)√1274 =
= (1/2)*7√26 = (7/2)√26 ≈ 17,846568 кв.ед.
4. Объем пирамиды V = (1/6)*[A1A2xA1A3]*A1A4 =
= (1/6)* (-28; 21; 7)*(-3; 1; 1) = (1/6)*(84 +21 + 7) = 112/6 = 56/3 ≈ 18,6667 куб.ед.
5. Длину высоты, опущенной из вершины А4 на грань А1А2А3;
H = 3V/S(A1A2A3) = 3*(56/3)/((7/2)√26) = 56√26/91 ≈ 3,137858.
6. Уравнение ребра А1А4.
Точка A1(4; 7; 8), вектор А1А4 = (-3; 1; 1), его модуль √(9+1+1) =√11.
Уравнение А1А4: (x - 4)/(-3) = (y - 7)/1 = (z - 8)/1.
7. Уравнение плоскости А1А2А3.
Используя найденное векторное произведение А1А2 на А1А3:
-28x + 21y + 7z - 91 = 0 или, сократив на (-7):
4x - 3y - z + 13 = 0.
8. Угол между ребром А1А4 и плоскостью А1А2А3;
Вектор А1А4 = (-3; 1; 1), модуль √11.
Вектор плоскости (-28;21; 7), модуль √1274.
sin a = |-3*-28+1*21+1*7)/(√11*√1274) = 0,9460998.
Угол равен 1,240974 радиан или 71,10256 градуса.
2000-600=1400 кг капусты
2000*2=4000 кг прочие овощи
4000+2000+1400=7400 кг=74 ц всего овощей