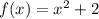Математика: Найдите остаток от деления числа n=1*2*3*4*5*6*7*8*9*10+1 . на 18

Найдите остаток от деления числа n=123456789*10+1 . на 18

👇

Ответ:

anaradocina

22.11.2022

2*9 делится на 18, поэтому и 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 делится на 18 (то есть дает остаток 0 при делении на 18).
1 дает остаток 1 при делении на 18, поэтому
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 + 1 дает остаток 0+1=1 при делении на 18

ответ: 1

4,4(38 оценок)

Открыть все ответы

Ответ:

Kotik77789

22.11.2022

Пусть функция f(x)=x^2+2

определена на множестве E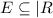 $E\subseteq |R$
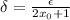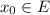Пусть $\delta=\frac{\epsilon}{2x_0+1}$ где $x_0 \in E$ .
Понятно, что для любого

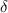на области $\delta$ от x_0

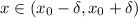(то есть: $x \in 
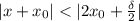(x_0-\delta,x_0+\delta)$ ) выполняется $|x+x_0|<|2x_0+ \frac{\delta}{2}|$ .
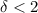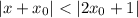Следовательно, для $\delta<2$ , выполняется |x+x_0|<|2x_0+1|

.

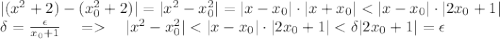
$|(x^2+2)-(x_0^2+2)|=|x^2-x_0^2|=|x-x_0|\cdot|x+x_0| < |x-x_0|\cdot|2x_0+1| \\
\delta= \frac{\epsilon}{x_0+1} \ \ \ = \ \ \ |x^2-x_0^2|< |x-x_0|\cdot|2x_0+1|<\delta|2x_0+1|=\epsilon$

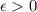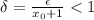Получили, что для любого $\epsilon 0$ есть $\delta=\frac{\epsilon}{x_0+1}<1$ , на области которой выполняется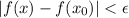 $|f(x)-f(x_0)|<\epsilon$
(Проще говоря:
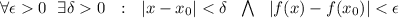$\forall
 \epsilon0 \ \ \exists\delta0 \ \ : \ \ |x-x_0|<\delta \ \ 
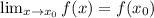\bigwedge \ \ |f(x)-f(x_0)|<\epsilon$ ). Следовательно - $\lim_{x 
\to x_0} f(x)=f(x_0)$ .
Что и требовалось доказать.
Для x_0=-1

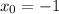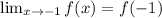нужно отдельно доказать предел $\lim_{x \to -1} f(x)=f(-1)$ .

Теперь в чём проблема самого вопроса: мы только что доказали непрерывность функции на любом подмножестве

. Но! Множество натуральных чисел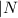

тоже подмножество

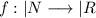, значит $f:|N \longrightarrow |R$ тоже непрерывна, получается - доказали что

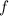непрерывна на области определения? Известно, что 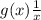$g(x) \frac{1}{x}$ тоже непрерывна на области определения, но

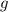, понятное дело, не определена на

!
Потому вопрос, ИМХО, поставлен не верно (претензия не к тебе, а скорее к преподавателям твоим). Правильно задать вопрос указывая то множесто точек, которое интересует: к примеру "непрерывна на

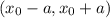" или, "непрерывна на отрезке (x_0-a,x_0+a)

"...
Тем более, что есть понятие "равномерная непрерывность" - свойство области, а не так, как "непрерывность" - свойство точки. Отсюда и непонимание.
А то получается: спрашивают об области, а проверяют точку.
Будут вопросы - пиши.

P.S. Исправил ошибки в наборе символов. Текста много :)

4,7(52 оценок)

Ответ:

Brain111t

22.11.2022

Здравствуйте, дорогой водитель! Мне очень нужно с Вами поговорить о безопасном переходе людей по пешеходной дорожке. Ведь вы знаете, что белые полоски на дорогое называются «зеброй». А до «зебры» стоит знак, где в белом треугольнике идет человек по пешеходному переходу. И только здесь можно уверенно перейти дорогу. По «зебре» переходят дорогу и взрослые, и школьники, и даже очень пожилые люди. Бабушки и дедушки не могут бегать, плохо видят, и плохо слышат.

Белые полоски видны издалека, у вас есть время, чтобы сбавить скорость и убедиться, что дорогу ни кто не переходит. Или заметив людей на пешеходном переходе притормозить и подождать пока все люди перейдут дорогу. Представьте себе ситуацию, что вышла ваша пожилая мама и маленький ваш сыночек. Они идут по «зебре», а вы не сбавляете скорость. Это же трагедия! В лучшем случае они попадут в больницу с травмами, а в худшем…. даже подумать страшно!...

Поэтому, очень Вас соблюдать все Правила безопасного движения, а я буду соблюдать свои Правила пешехода.

Дорогой водитель, помните, вас и меня ждут дома родные и близкие!

4,5(99 оценок)

Это интересно:

Праздники-и-традиции

18.06.2022

Как подобрать идеальный подарок для папы...

Компьютеры-и-электроника

21.07.2020

Как создать газету в Microsoft Word за несколько минут...

Стиль-и-уход-за-собой

31.01.2022