1. Числа, используемые при счёте.
2. Часть отрезка, ограниченная двумя точками.
4. Переместительный (коммутативный) закон сложения: m + n = n + m . Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m . Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k . Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k . Произведение не зависит от группировки его сомножителей.
Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k .
5. (a+b)*c=a*c+b*c
6. Уравнение – это равенство, содержащее одну или несколько переменных.
7. Вычислить значение перемннной.
11. Приводим к одному знаменателю. У какой дроби числитель больше числителя другой дроби, та и больше.
15. Работаем с числителями.
0,99144
Пошаговое объяснение:
Для решения задачи воспользуемся формулой Бернулли для повторных испытаний. Пусть вероятность изделия оказаться бракованным это p=0,1. Вероятность изделия оказаться хорошим это q=0,9.
Партия будет принята без сплошного контроля, если из пяти изделий не будет вообще бракованных, либо одно бракованное, либо - два.
Найдем по очереди вероятности каждого из подходящих исходов:
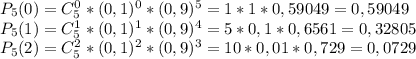
Просуммируем полученные вероятности:
0,59049+0,32805+0,0729=0,99144
Это и будет вероятность того, что партия будет принята без сплошного контроля.