8
Пошаговое объяснение:
Бассейн примем за 1 (одна целая часть).
Тогда:
1 : 12 = 1/12 часть бассейна за одну минуту заполнят первый и второй насосы
1 : 10 = 1/10 часть бассейна за одну минуту заполнят второй и третий насосы
1 : 15 = 1/15 часть бассейна за одну минуту заполнят первый и третий насосы.
Работая вместе, за одну минуту два первых, два вторых и два третьих насоса (каждый учтен дважды) заполнят:
1/12 + 1/10 + 1/15 = (5+6+4)/60 = 15/60 = 1/4 часть бассейна
Но так как каждый из насосов был учтен два раза, первый, второй и третий насосы, работая вместе, могут заполнить 1 бассейн за:
1 : 1/4 * 2 = 1*4*2 = 8 минут.
Или так:
НОК чисел 12, 10 и 15 равно 60.
За 60 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят:
60:12+60:10+60:15 = 5+6+4 = 15 бассейнов.
Следовательно, работая одновременно, первый, второй и третий насосы заполнят 7,5 бассейнов за 60 минут. Значит, 1 бассейн три насоса заполнят за 60 : 7,5 = 8 минут.
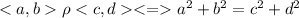
докажем, что ρ является отношением эквивалентности.
1) рефлексивность: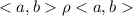 
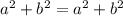
2) симметричность: если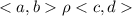 
то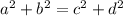 
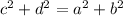
то есть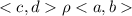 
3) транзитивность: если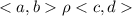 
и 
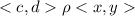, то
,
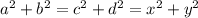то есть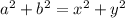 
то есть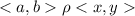 
На координатной плоскости: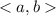 
, если первый параметра a отождествить с вещественными числами оси Ox, а второй параметр b отождествить с вещественными числами оси Oy, тогда значениям a² + b² будет соответствовать окружность радиуса R≥0. То есть отношение эквивалентности ρ разбивает всю координатную плоскость на классы эквивалентности. Каждому классу эквивалентности соответствует окружность радиуса
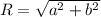с центром в начале координат.
Отсюда вероятность равна 45/91.
Пояснение: общее число всевозможных исходов есть сочетания из 14 по 3. Нужное количество исходов есть произведение (правило "И") сочетаний из 4 по 1 (один белый шар) на число сочетаний из 10 по 2 (чёрные шары, два).