Т.к. случайная величина X может принимать только два значения, то
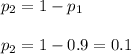
Математическое ожидание дискретной случайной величины равно сумме произведений значений этой величины на соответствующие вероятности
![M[X]=\sum\limits_{i=1}^{N}\,{x_i\,p_i}](/tpl/images/2004/8694/e38e8.png)
Для данной задачи
![M[X]=x_1\,p_1+x_2\,p_2](/tpl/images/2004/8694/1be08.png)
Дисперсия дискретной случайной величины равна разности суммы произведений квадратов значений этой величины на соответствующие вероятности и квадрата математического ожидания
![D[X]=\sum\limits_{i=1}^{N}\,{x_i^2\,p_i}-(M[X])^2](/tpl/images/2004/8694/0b48e.png)
Для данной задачи
![D[X]=x_1^2\,p_1+x_2^2\,p_2-(M[X])^2](/tpl/images/2004/8694/6c44c.png)
Имеем 2 уравнения с двумя неизвестными величинами. Составим и решим систему уравнений
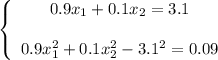
Решением данной системы являются 2 пары значений
Первая пара значений:
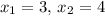
Закон распределения
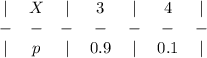
Вторая пара значений
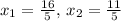
Закон распределения
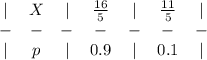
б) 30
в) 1/14
г) 1/15
д) 60
е) 6
ж) 1/125
з) 9/10
и) 1/150
к) 50
л) 4
м) 1