96 см² площадь боковой поверхности призмы.
Пошаговое объяснение:
В прямоугольной призме, основанием которой является прямоугольный треугольник площадь боковой поверхности (S) находится путем сложения площадей трех боковых граней - прямоугольников.
S=S₁+S₂+S₃
S₁=аh, где а - катет основания, h - боковое ребро (высота призмы)
S₂=вh, где в - катет основания, h - боковое ребро (высота призмы)
S₃=сh, где с - гипотенуза основания, h - боковое ребро (высота призмы)
S₁=4×8=32 см²
S₂=3×8=24 см².
Согласно теореме Пифагора гипотенуза с=√(а²+в²)
с=√(4²+3³)=5 см
S₃=5×8=40 см²
S=32+24+40=96 см²
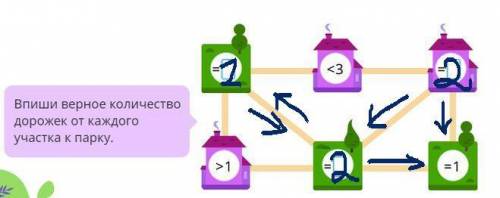
У нас шесть парков, условно обозначим их цифрами от одного до шести. Первый, третий и пятый парки у нас без числовых обозначений: будем туда их вписывать.
Парк номер один - в левом верхнем углу - к центральному нижнему (пятому) имеет лишь одну дорожку. В первый парк вписываем цифру один.
От пятого парка - внизу в центре - будут отходить уже две дорожки, потому что одна пойдет направо в шестой, а вторая реверсом в первый парк. В пятый парк вписываем цифру два.
От третьего парка (в правом верхнем углу) также прокладываются две дорожки, одна из которых идет к шестому (прям под ним), а вторая - по диагонали к пятому. В третий парк записываем двоечку.
т.к. сумма числа и есть это число только разложение.