Question

Рассаду цветов и распределили их по трём клумбам.на первой клумбе посадили 1/3 всех кустиков рассады,на второй 1/3 остатка,на третьей 1/3 нового остатка рассады. после этого осталось 24 кустика рассады. сколько всего рассады
цветов ?

Answer 1

Последний остаток - 1

1-1/3=2/3  - 24 куста-третий остаток

24 : 2 * 3 = 36 - второй остаток

36 : 2 * 3 = 54 - первый остаток

54 : 2 * 3 = 81- всего кустов

ответ: привезли 81куст рассады

Проверка:

81:3=27

81-27=54

54:3=18

54-18=36

36:3=12

36-12=24 - последний остаток

Answer 2

Примем за 1 (целую) часть общее количество кустов рассады, тогда

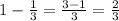1) $1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}$ (часть) - рассады осталась не посаженная.

2) 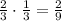$\frac{2}{3}\cdot\frac{1}{3}=\frac{2}{9}$ (часть) - рассады посадили на вторую клумбу.

3) 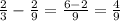$\frac{2}{3}-\frac{2}{9}=\frac{6-2}{9}=\frac{4}{9}$ (часть) - рассады осталось посадить.

4) 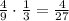$\frac{4}{9}\cdot\frac{1}{3}=\frac{4}{27}$ (часть) - рассады посадили на третьей клумбе.

5) 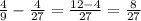$\frac{4}{9}-\frac{4}{27}=\frac{12-4}{27}=\frac{8}{27}$ (часть) - рассады осталась не посаженной.

6) 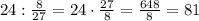$24:\frac{8}{27}=24\cdot\frac{27}{8}=\frac{648}{8}=81$ (к.) - рассады цветов привезли Примем за 1 (целую) часть общее количество кустов рассады, тогда

1) 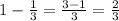$1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}$ (часть) - рассады от нового остатка рассады составляет 24 куста.

2) 24:2=12 (к.) - рассады цветов посадили на третьей клумбе, что соответствует 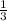$\frac{1}{3}$ части рассады от нового остатка.

3) 12·3=36 (к.) - новый остаток рассады, что соответствует 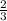$\frac{2}{3}$ части остатка рассады.

4) 36:2=18 (к.)  - рассады цветов посадили на второй клумбе, что соответствует 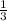$\frac{1}{3}$ части остатка рассады.

5) 18·3=54 (к.) - остаток рассады, что соответствует 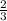$\frac{2}{3}$ части всей рассады.

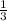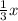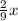6) 54:2=27 (к.) - рассады цветов посадили на первой клумбе, что соответствует  $\frac{1}{3}$ части всей рассады Предположим, что всего привезли х кустов рассады цветов, тогда на первой клумбе посадили $\frac{1}{3}x$ кустов рассады, следовательно, на второй клумбе посадили $\frac{1}{3}(x-\frac{1}{3}x)$ или $\frac{2}{9}x$ кустов рассады, а на третьей 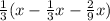$\frac{1}{3}(x-\frac{1}{3}x-\frac{2}{9}x)$ или $\frac{4}{27}x$, 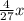после этого осталось 24 куста рассады

согласно этим данным составим и решим уравнение:

$\frac{1}{3}x+\frac{2}{9}x+\frac{4}{27}x+24=x$

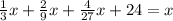
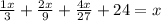$\frac{1x}{3}+\frac{2x}{9}+\frac{4x}{27}+24=x$ /·27

умножаем на 27 для того, чтобы избавиться от знаменателей

$9x+6x+4x+648=27x$

$19x+648=27x$

$27x-19x=648$

$8x=648$

$x=648:8$

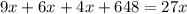
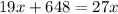
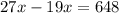
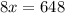
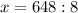
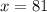$x=81$ (к.) - рассады цветов привезли.

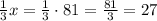$\frac{1}{3}x=\frac{1}{3}\cdot81=\frac{81}{3}=27$ (к.) - рассады цветов посадили на первой клумбе.

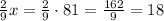$\frac{2}{9}x=\frac{2}{9}\cdot81=\frac{162}{9}=18$ (к.) - рассады цветов посадили на второй клумбе.

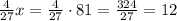$\frac{4}{27}x=\frac{4}{27}\cdot81=\frac{324}{27}=12$ (к.) - рассады цветов посадили на третьей клумбе.

ответ: привезли 81 куст рассады цветов.

Проверка:

27+18+12+24=81 (к.) - рассады цветов всего.