Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
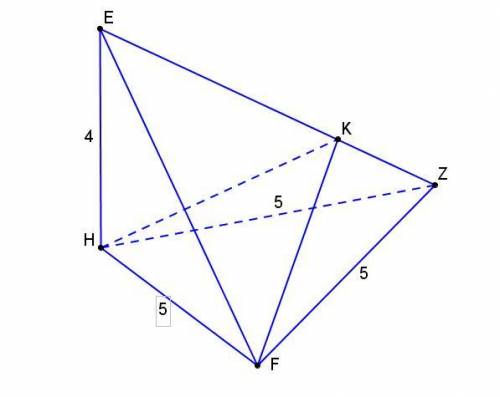
В данной задаче - это угол FKH.
Отрезки FK и HK это высоты треугольников боковых граней ZEF и HZE.
Находим их длины.
Треугольник ZEF равнобедренный. Боковые стороны равны
FE = ZE = √(5² + 4²) = √(25 + 16) = √41.
Его высота к стороне FZ = √(41 - (5/2)²) = √139/2.
Тогда высота FK к стороне ZE равна (√139/2*5)/√41 = 2,5√(139/41).
Высота НК к стороне EZ равна (4*5)/√41 = 20/√41.
Стороны треугольника HKF определены, по теореме косинусов находим угол HKF.
cos HKF = ((20/√41)² + (2,5√(139/41))² - 5²)/(2*(20/√41)*(2,5√(139/41)) = 0,206746052
Угол HKF равен 1,3626 радиан или 78,0683 градуса.
АB = √((Хв-Ха)²+(Ув-Уа)²+(Zв-Zа)²)= √9 =3.
BC = √((Хс-Хв)²+(Ус-Ув)²+(Zс-Zв)²) = √8 ≈ 2,82843.
АС = √((Хс-Ха)²+(Ус-Уа)²+(Zс-Zа)²) = √21 ≈ 4,58258.
По формуле Герона находим площадь.
S = √(p(p-a)(p-b)(p-c)).
Полупериметр р = 5,20550141.
Подставив данные. находим S = 4,12311.
Можно применить векторный
x y z
Вектор АВ={xB-xA, yB-yA, zB-zA} 2 2 -1
Вектор АC={xC-xA, yC-yA, zC-zA} 2 4 1.
Произведение векторов a × b = {aybz - azby; azbx - axbz; axby - aybx} Площадь a1 a2 a3
S = ABC [AB ; AC]= 6 -4 4
S = (1/2)√(6²+(-4)²+4²) = 4,123106.