1. 10л; 2. 126 яблок 3
Пошаговое объяснение:
Задача 1.
60л : 10мин = 6л/мин - скорость наполнения
60л : 15 мин = 4л/мин - скорость опорожнения
6л/мин - 4л/мин = 2л/мин - оказывается в баке за 1 мин, если открыть обе трубы
2л/мин · 5мин = 10л - окажется в баке через 5мин при обеих открытых трубах.
Задача 2.
х - яблок принесла крестьянка
0,5х + 1 - продала она 1-му покупателю
х - 0,5х - 1 = 0,5х - 1 - осталось в корзине после 1-го покупателя
0,25х - 0,5 + 1 = 0,25х + 0,5 -продала крестьянка 2-му покупателю
0,5х - 1 - 0,25х - 0,5 = 0,25х - 1,5 - осталось в корзине после 2-го покупателя.
0,125х - 0,75 + 1 = 0,125х + 0,25 - продала крестьянка 3-му покупателю
0,25х - 1,5 - 0,125х - 0,25 = 0,125х - 1,75 - осталось в корзине после 3-го покупателя
0, 0625х - 0,875 + 1 = 0,0625х + 0,125 - продала крестьянка 4-му покупателю
0,125х - 1,75 - 0,0625х - 0,125 = 0,0625х - 1,875 - осталось в корзине после 4-го покупателя
0,03125х - 0,9375 + 1 = 0,03125х + 0,0625 - продала крестьянка 5-му покупателю
0,0625х - 1,875 - 0,03125х - 0,0625 = 0,03125х - 1,9375 - осталось в корзине после 5-го покупателя.
0,015625х - 0,96875 + 1 = 0,015625х +0,03125 - продала крестьянка 6-му покупателю
0,015625х + 0,03125 + 0,03125х + 0,0625 + 0,0625х + 0,125 + 0,125х + 0,25+ 0,25х + 0,5 + 0,5х + 1 = х
0,984375х + 1,96875 = х
0,015625х = 1,96875
х = 126
Задача 3.
Если Юра за завтраком съел 1 конфету, то тогда за обедом и ужином - 9 конфет (соответственно 1 и 8; 2 и 7; 3 и 6; 4 и 5; и наоборот 8 и 1; ... и так далее). Получается, что за 1 раз он съедал не менее 4-х конфет
Если Юра за завтраком съел 2 конфеты, то тогда за обедом и ужином - 8 конфет (соответственно 1 и 7; 2 и 6; 3 и 5; 4 и 4; и наоборот 7 и 1; ... и так далее). Получается, что за 1 раз он съедал не менее 4-х конфет
Если Юра за завтраком съел 3 конфеты, то тогда за обедом и ужином - 7 конфет (соответственно 1 и 6; 2 и 5; 3 и 4; и наоборот 6 и 1; ... и так далее). Получается, что за 1 раз он съедал не менее 4-х конфет
Следующие допущения, что он съел 4 конфеты за завтраком, 5 конфет и далее до 9 не имеет смысла рассматривать, так как уже получается, что за завтраком он съел 4 или более конфет.
Таким образом, можно считать доказанным, что если Юра за три приёма съедал 10 конфет, то за 1 приём - не менее 4-х.
Пошаговое объяснение:
запишем уравнение в виде
2х²+ух-(у²+5)=0
и решим его относительно х
d=y²+4*2(y²+5)=y²+8y²+40=9y²+40
x₁₋₂=(-y±√d)/4
чтобы х и у были целыми числами необходимо чтобы корень из дискриминанта был целым числом и выражение -y±√d было кратно 4
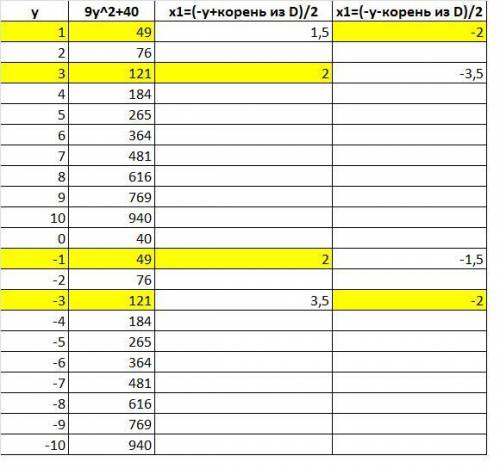
решим задачу методом подбора
придавая у значения равные целым числам будем вычислять дискриминант, и если он целый то вычислим корни если они целые то все хорошо
для примера рассмотрим целые значения у ∈[-10;10]
результат вычислений в приложении
полученные решения
(-2;1) (2;3) (2;-1) (-2;-3)
проверка
-2-1+8=5
6-9+8=5
-2-1+8=5
6-9+8=5
примечания
расчеты произведены в екселе,
если есть время и желание можно продолжить процесс поиска других корней но выскажу гипотезу что больше целочисленных решений нет
ax + by + cz + d = 0
коэффициенты (а, b, c) являются координатами вектора n, ортогонального плоскости. Так что мы имеем два вектора n1(1, -2, 3) и n2(1, 1, -5), которые ортогональны нашим плоскостям. Т. к. наша прямая лежит одновременно в обоих плоскостях, то она ортогональна обоим векторам n1 и n2. Соответственно направляющим вектором этой прямой может быть вектор, равный векторному произведению [n1, n2]. Итак, составляете матрицу векторного произведения, раскладываете ее по строке с символами i j k и получаете координаты направляющего вектора.
2. Т. к. плоскость параллельна оси ОХ, то на искомой плоскости всегда можно построить вектор с координатами (1, 0, 0). Действительно, предположим мы возьмем на плоскости точку М с координатами (а, b, c). Тогда на плоскости имеется и точка М1(a+1, b, c). Ведь если мы проведем из точки М (a, b, c) прямую, параллельную оси ОХ, то у всех точек этой прямой координаты у и z будут одинаковы, а изменяться будет лишь координата х.
Найдем координаты вектора ММ1(a +1 - a, b - b, с - с) = (1, 0, 0)
3. Теперь найдем точку, принадлежащую искомой плоскости. Предположим эта точка лежит на прямой пересечения двух плоскостей x-2y+3z-4=0 и x+y-5z+9=0. Предположим также, что координата z этой точки равна 0. Тогда, подставив в уравнения плоскостей z = 0 получим систему уравнений:
x - 2y - 4 = 0
x + y + 9 = 0
Решая эту систему получаем:
х = -14/3
y = -13/3
Итак мы нашли координаты точки А (-14/3, -13/3, 0), которая принадлежит искомой плоскости.
4. Теперь возьмем на искомой плоскости произвольную точку Х (х, y, z) и найдем координаты вектора АХ (x +14/3, y + 13/3, z) который пробегает все точки плоскости.
5. Таким образом у нас есть 3 вектора: направляющий вектор прямой, координаты которого Вы нашли в п. 1, вектор ММ1(1, 0, 0) и вектор АХ (x +14/3, y + 13/3, z). Все эти векторы компланарны. А это значит, что их смешанное произведение равно 0. Теперь составляем матрицу смешанного произведения этих векторов, поставив на первую строчку координаты вектора АХ (x +14/3, y + 13/3, z). Далее разложив матрицу по первой строке, приведя коэффициенты при х, у, z и приравняв полученное выражение к 0 Вы получите искомое уравнение плоскости.