Применяется классификация географических карт по территориальному признаку, содержанию, предназначению и масштабу. По охвату территории различают карты мира, морей и океанов, материков, стран, областей, регионов. Наибольшим спросом пользуются общегеографические карты, на которые нанесены формы рельефа земной поверхности, гидрографические объекты, населенные пункты, границы стран. Все другие карты называются тематическими, так как на них подробно указаны определенные элементы из общегеографической карты, например, рельеф, климатические пояса, почвенный покров, дороги, распространение растений, т.д. По назначению карты делят на справочные, туристические, учебные, т.д. Существует классификация карт по масштабу. Выделяют крупномасштабные, выполненные в масштабах более 1:200000; мелкомасштабные, созданные в масштабах менее 1:1000000; среднемасштабные делают в масштабах от 1:200000 до 1:1000000.
На крупномасштабных топографических картах масштаб является постоянной величиной на всех участках карты. Рельеф на данных картах обозначен в форме горизонталей, соединяющих точки на одной высоте над уровнем моря. На мелкомасштабных картах в любом случае появляются искажения площадей, углов и расстояний, так как нет возможности развернуть уменьшенную поверхность земного шара на одной плоскости. Поэтому при составлении карт прибегают к картографическим проекциям – специальным методикам развертки на плоскости земной поверхности.
7. 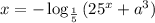
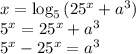
Пусть 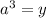 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию 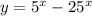 :
:
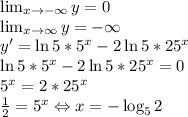
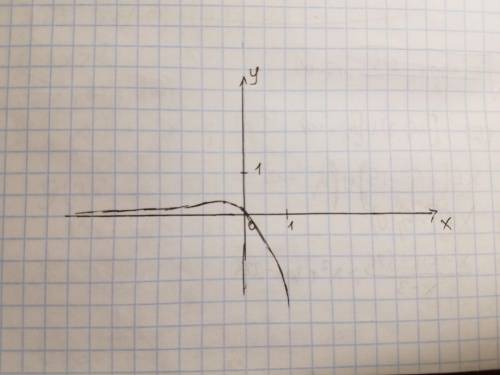
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно 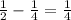 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
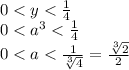
ответ: ![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
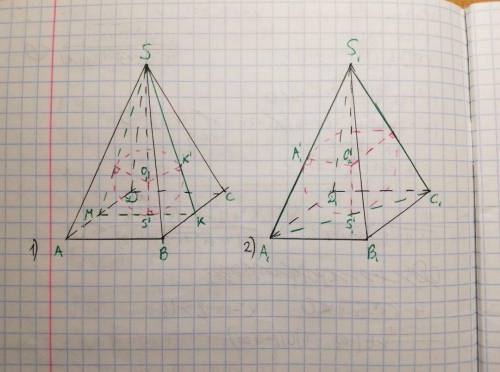
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
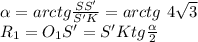
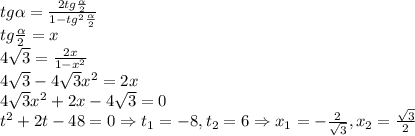
Учитывая, что угол находится в первой четверти, 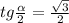
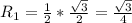
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
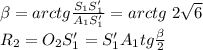
Решая аналогичное уравнение, получаем 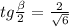
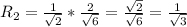
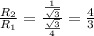
ответ: 4 : 3
1)8:30-8:00=30(мин.)-он шёл от дома до школы.
2)1км500м=1500м
3)1500м:30мин.=50(м)
ответ:50м\мин.