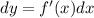 или
или 

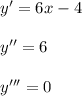


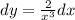
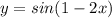




Скорость Оли = 12 км/час, потому что за пол часа она проехала 6 км.
Скорость Маши = 10 км/час. Она едет медленнее Оли на 20%.
Это неправильно. Выше видно, что наоборот у Оли выше.
Оля едет со скоростью 12 км/час, 10 минут - это 1/6 часа, значит она проедет 2 км (12 : 6 = 2)
Маша едет со скоростью 10 км/час, 12 минут - это 1/5 часа, значит она проедет 2 км (10 : 5 = 2)
Что и требовалось доказать.
Маша проедет за 12 минут 2 км, как мы выяснили раньше. и ещё за час она проедет 10 км, исходя из её скорости 10 км/час, то в сумме она проедет 2 + 10 = 12 км.
Зато Оля ездит на велике быстрей. Со скоростью 12 км в час. Столько она и проедет догнав Машу.
Что и требовалось доказать. Это верное заключе
1) 100 7/10+2 3/19=100 133/190+2 30/190=102 160/190=51 80/95=51 16/19
2) 51 16/19-4 3/95=51 80/95-4 3/95=47 77/95