ответ: Ноль встречается пять раз.
Пошаговое объяснение:
|5| + |-7| - 1 = 5 + 7 - 1 = 11 чисел между -7 и 5.
С учётом 5 и -7, получаем 13 чисел.
Обратим внимание, что любая цепочка чисел (от -7 до 5, каждое следующее число цепочки увеличивается на 1) в заданном прямоугольнике будет иметь длину в 13 клеток. И возможно это только если -7 и 5 стоят в противоположных углах прямоугольника (5 + 9 - 1 = 13). В противном случае будет появляться клетка, в которой соседние числа отличаются более, чем на 1.
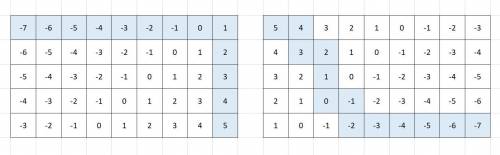
Заполним произвольно одну такую цепочку. Затем находим клетки, рядом с которыми стоят 2 числа. По правилу заполняем эту клетку.
Например на левом прямоугольнике такая клетка одна -- около верхнего правого угла. Между 0 и 2 стоит число 1. Оно как раз отличается на единицу от 0 или 2. Вписываем 1 в клетку.
Продолжая этот процесс, прямоугольник заполнится однозначно.
На рисунке представлено 2 примера, как от произвольной цепочки получается заполненный прямоугольник. Отсюда вытекает, что всего будет пять нулей.
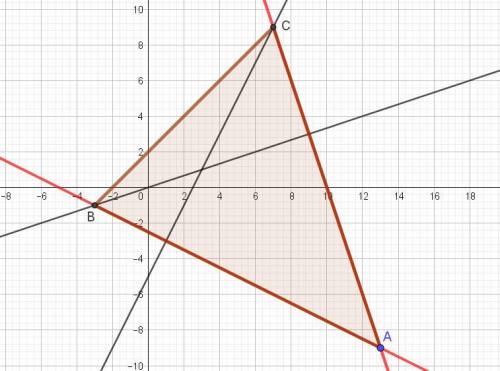
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
{ -x + 2y = 5
{ -x + 5z = 2
{ x = 3
{ x = 3
{ y = (5+x)/2 = 4
{ z = (2+x)/5 = 1
d(3; 4; 1)