ДАНО: y = (x+4)*(x² + 3*x + 2)/(x+1)
Пошаговое объяснение:
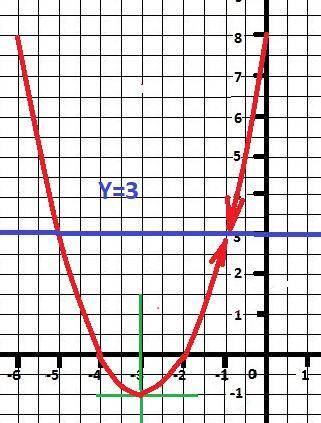
Сразу видим разрыв функции при Х = -1 (х+1 ≠ 0)
Разложим числитель на произведение решив квадратное уравнение. Корни уравнения: х1 = -1 и х2 = - 2
(x+4)*(x+2)*(x+1) - числитель.
После сокращения со знаменателем получим уравнение графика.
y = (x+4)*(x+2) = x² + 6*x + 8, но которое не существует при Х= -1.
Вычисляем координату точки разрыва при х = -1.
у(-1) = 1 - 6 + 8 = +3
Вот и прямая Y=m должна проходит через эту точку.
ОТВЕТ: m = 3
Рисунок с графиком функции в приложении.
36
Пошаговое объяснение:
Чтобы решить задачу, посмотрим, как устроен еженедельник из задачи. Его конструкция точно такая же, как и обычной ученической тетради. Берется несколько листов бумаги, по оси симметрии сцепляются скобками, и полученная пачка сгибается пополам. В результате, на 1 исходном листе получается 4 страницы, причем левый полулист по счету с начала, будет такой же как и правый полулист по счету с конца (в обратном направлении).
В нашей задаче на листе встречаются страницы с номерами 14 и 23, значит на этом же листе есть страницы №13 и №24 (т.к. начинается нумерация страниц с нечетного числа и заканчивается чётным). Очевидно, что 14 - это левая часть листа - полулист под номером 14:2=7.
Значит правая часть листа будет седьмой с конца.
Значит осталось еще правых 6 полулистов до конца еженедельника.
6 полулистов это 6*2=12 страниц.
24+12=36
Значит страница №36 - последняя в еженедельнике и всего их 36.
Задача решается именно для такой конструкции еженедельника, как указано выше. Для клеенного издания условие не подходит. т.к. на одном листе там обязательно будут соседние страницы.
Квадрат 2x2: 1 сторона клетки = 1 спичка. 1 сторона квадрата = 2 спички.
У квадрата 4 стороны, значит: 4*2 = 8. и 4 спички внутри. на весь квадрат 8+4 = 12. Верно. Как и в условиях.
Квадрат 5х5: 1 ст. кл. = 1 спичка. 1 сторона квадрата = 5 спичек.
У квадрата 4 стороны, значит: 4*5 = 20. и 40 спичек внутри. на весь квадрат 20+40=60 спичек уйдет на клетчатый квадрат 5 х 5.
Лучше всего прочертить на листке, чтобы наглядно видеть каждую спичку