370.
РΔАВС=17/20м
АВ=17м/50
ВС- на 9м/50 меньше АВ
АС=?
ВС=17/50-9/50=8/50=4/25
АС= Р-АВ-ВС=17/20-17/50-8/50=17/20-25/50=17/20-1/2=17/20-10/20=7/20/м/=35см
371
1- (1/3)ч
2- на (1/6)ч больше
3- на 7/12 меньше. чем на 1и 2 вместе.
? времени на чтение всей книги.
1)1/3+1/6=2/6+1/6=3/6=1/2/ч/- на второй рассказ ушло времени.
2) (1/3+1/2)-7/12=5/6-7/12=10/12-6/12=4/12=1/3/ч/ -на 3 рассказ ушло времени.
3)1/3 +1/2 +1/3=2/3+1/2=4/6 +3/6=7/6= 1 1/6/ч/ или это 1час и 10 минут ушло времени на три рассказа.
372
Оля затратила
4/5-(5/12+1/3)=4/5-(5/12+4/12)=4/5-9/12=4/5-3/4=(16-15)/20=1/20 /часа/, или это 3 минуты.
a) x∈(-∞;-2]∪(-1;1)∪[7;+∞)
b) x∈(0;1]
c) x∈[0;π²/4]∪[(-π/2+2kπ)²; (π/2+2kπ)²], k∈N
Пошаговое объяснение:
a) y=arcsin[(5x+13)/(x²-1)]
x²-1≠0⇒x≠±1
-1≤(5x+13)/(x²-1)≤1
1) (5x+13)/(x²-1)≤1
1-(5x+13)/(x²-1)≥0
[(x²-1)-(5x+13)]/(x²-1)≥0
(x²-5x-14)/(x²-1)≥0⇔(x²-5x-14)·(x²-1)≥0, x≠±1
(x+2)(x+1)(x-1)(x-7)≥0
Решая методом интервалов, имеем
x∈(-∞;-2]∪(-1;1)∪[7;+∞)
b) y=arcsin√(1-x)+arccos√x+∛(x-1)+lnx
1) arcsin√(1-x) имеет смысл при 1-x≥0 ∩ √(1-x)≤1⇒x∈[0;1]
arccos√x имеет смысл при x≥0 ∩ √x≤1⇒x∈[0;1]
∛(x-1) имеет смысл при ∀x∈R
lnx имеет смысл при x>0⇒x∈(0;+∞)
[0;1]∩[0;1]∩R∩(0;+∞)=(0;1]
c)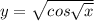 
√x имеет смысл при x≥0
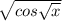имеет смысл при cos√x≥0
cost≥0⇒-π/2+2kπ≤t≤π/2+2kπ
-π/2+2kπ≤√x≤π/2+2kπ
при к отрицательном решения нет, так как 0≤√x
при к=0, 0≤√x≤π/2⇒0≤x≤(π/2)²⇒0≤x≤π²/4
при к≥1 -π/2+2kπ≤√x≤π/2+2kπ⇒(-π/2+2kπ)²≤x≤(π/2+2kπ)²
x∈[0;π²/4]∪[(-π/2+2kπ)²; (π/2+2kπ)²], k∈N
d)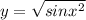 
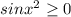
2kπ≤x²≤π+2kπ, k=0;1;2;3;4;...
при к=0, х²≤π=>-√π≤х≤√π
при к €N, решаем двойные неравенства вида 2kπ≤x²≤π+2kπ, которые по сути являются системой неравенств 2kπ≤x², x²≤π+2kπ. Решением их является пересечение множеств их решений
