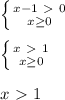
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
ответ: – 8.
Пример 3. Решите уравнение .
. Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
ответ: 3.
Пример 4. Решите систему
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
ответ: (1; 1).
Замечание. Если неизвестные системы х и у, то ответ можно записать в виде ко
Пошаговое объяснение:
надеюсь правильно
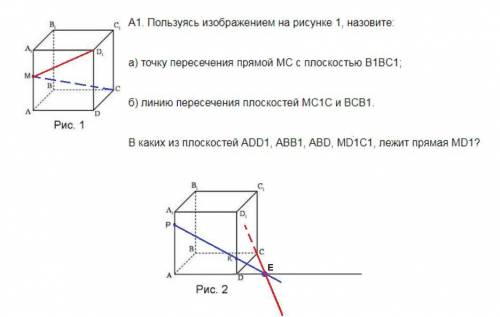
А1.
а) МС ∩ (В₁ВС) = С;
б) (МС₁С) ∩ (ВСВ₁) = СС₁, так как обе точки - С и С₁ - принадлежат двум плоскостям.
Прямая MD₁ лежит в тех плоскостях, в которых лежат обе точки - М и D₁: (ADD₁), (MD₁C₁)
A2.
а) РК лежит в плоскости (АА₁D), эта плоскость пересекает (АВС) по прямой AD. Поэтому находим точку пересечения прямых AD и РК - точку Е. Это и есть точка пересечения прямой РК и плоскости (АВС).
РК ∩ (АВС) = Е.
б) Чтобы построить линию пересечения плоскостей (РКС) и (ADC) надо найти или построить две точки, принадлежащие этим двум плоскостям.
Точка Е лежит на прямых РК и AD, значит принадлежит двум плоскостям. Точка С принадлежит плоскости (РКС), это видно из названия, и плоскости (ADC). Значит ЕС - искомая прямая.
(РКС) ∩ (ADC) = ЕС.