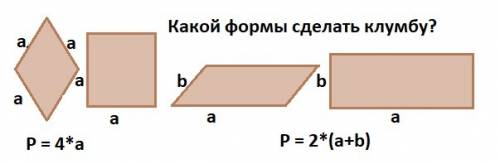
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
1) К численному интегрированию чаще всего прибегают, когда приходится вычислять интегралы от функций, заданных таблично, или когда непосредственное интегрирование функции затруднительно.
2) К численному интегрированию чаще всего прибегают, когда приходится вычислять значения функции в промежуточных точках, при этом данная функция задана в табличном виде и аналитическое выражение функции неизвестно.
3) К численному интегрированию чаще всего прибегают, когда требуется определить допустимую погрешность аргументов по допустимой погрешности функции.