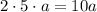
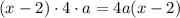
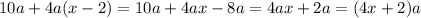
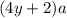. По условию она увеличилась в k раз. Получаем равенство: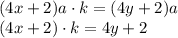
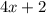и выражение 
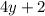при делении на 4 дает остаток 2. Однако при четном 
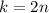возникает противоречие: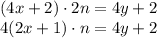
Если речь идёт о кратности чисел, то рассматривается целые числа. Поэтому определим целые решения неравенств. Z - множество целых чисел.
1) 120 < х < 170
x∈[121; 169], x∈Z
Наименьшее число из [121; 169], которое кратно 9, это 126 (по признаку делимости: сумма цифр 9 делится на 9). Каждое следующее кратное число больше предыдущего кратного числа на 9:
126; 135; 144; 153; 162
2) 81 < y ≤ 99
x∈[82; 99], x∈Z
Наибольшее число из [82; 99], которое кратно 9, это 99 (по признаку делимости: сумма цифр 18 делится на 9). Каждое предыдущее кратное число меньше от следующего кратного числа на 9:
90; 99
3) 63 ≤ z ≤ 117
x∈[63; 117], x∈Z
Наименьшее число из [63; 117], которое кратно 9, это 63 (по признаку делимости: сумма цифр 9 делится на 9). Каждое следующее кратное число больше предыдущего кратного числа на 9:
63; 72; 81; 90; 99; 108; 117
