№459
1) 3/5 и 5/6 = 18/30 и 25/30
2) 6/11 и 4/9 = 54/99 и 44/99
3) 5/6 и 4/11 = 55/66 и 24/66
4) 7/18 и 1/6 = 7/18 и 3/18
5) 9/13 и 4/5 = 45/65 И 52/65
6) 5/7 и 3/4 = 20/28 и 21/28
7) 2/15 и 1/3 = 2/15 и 5/15
8) 5/8 и 3/4 = 10/16 и 12/16
№460
1) 1/2, 1/6, 2/3 = 3/6, 1/6, 4/6
2) 1/4, 5/7, 9/28 = 7/28, 20/28, 9/28
3) 1/5, 11/20, 3/10 = 4/20, 11/20, 6/20
4) 3/4, 7/8, 3/16 = 12/16, 14/16, 3/16
5) 2/3, 2/15, 4/5 = 10/15, 2/15, 12/15
6) 1/2, 1/9, 5/6 = 9/18, 2/18, 15/18
№461
1) 7/20 и 5/12 = 21/60 и 25/60
2) 11/24 и 1/30 = 330/720 и 24/720
3) 3/16 и 7/12 = 9/48 и 28/48
4) 11/18 и 7/12 = 22/36 и 21/36
5) 1/12 и 2/9 = 3/36 и 8/36
6) 4/21 и 13/28 = 16/84 и 39/84
7) 8/15 и 5/12 = 32/60 и 25/60
8) 7/30 и 1/12 = 84/360 и 30/360
я очень старался
ответ Чтобы представить смешанное число в виде неправильной дроби, нужно знаменатель умножить на целую часть числа, к полученному произведению прибавить числитель дробной части и записать эту сумму в числитель дроби. В знаменатель неправильной дроби записываем знаменатель дробной части смешанного числа.
знаменатель у нас -15
целое чило-4
числитель-7
15×4+7=67 это будет чилитель неправильной дроби
а знаменатель неправильной дроби записываем знаменатель дробной части смешанного числа-15
Представим смешанное число в виде неправильной дроби 4 7/15= 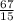
Пошаговое объяснение:
Первой дробью известной человечеству была половина, далее - треть. Древние египтян и вавилоняне имели специальные обозначения для дробей 13 и 23 , которые отличались от обозначения остальных дробей. Египтяне все дроби старались записать как суммы долей, то есть дробей вида 1n , за исключением единственной дроби - 23 . Но складывать такие дроби было неудобно. Также египтяне умножали и делили дроби.
Вавилоняне работали только с шестидесятеричными дробями. Так как знаменателями таких дробей служат числа 60, 602, 603 и т.п., то такие дроби, как 1/7, нельзя было точно выразить через шестидесятеричные. Выражали через подобные дроби приближенно.
Шестидесятеричные дроби заимствовали у Вавилона греческие и арабские математики и астрономы. Но возникали трудности при работе с натуральными числами, записанными в десятичной системе, и дробями, записанными в шестидесятеричной. Поэтому фламандский математик, механик и инженер Симон Стевин (1548 - 1620) предложил перейти к десятичным дробям.
Своей системой дробей отличался Древний Рим. Эта система основывалась на делении на 12 долей единицы веса, называемой асс. Двенадцатая доля асса называлась унция. В ходу были и следующие названия: "семис" - половина асса, "секстане" - шестая доля асса, "семиунция" - полунции, то есть 1/24 асса. Всего применялось 18 различных названий дробей. Для работы с такими дробями надо было помнить и таблицу сложения, и таблицу умножения. Для облегчения работы составлялись специальные таблицы. Недостатком такой системы было то, что в ней не было дробей со знаменателями 10 или 100, что затрудняло деление на 10, 100 и т.д. Для избежания указанных трудностей римляне стали использовать проценты.
В греческих сочинениях по математике дробей не встречалось, т.к. греческие ученые считали, что математика должна заниматься только целыми числами. Дроби в греческой науке появились благодаря музыке.
Запись дробей с числителем и знаменателем предложили в Индии, только знаменатель писали вверху, а числитель в внизу, а также не ставили черту дроби. Современную запись дробей предложили арабы. Фундамент теории обыкновенных дробей заложили греческие и индийские математики.
Впервые в Европе данный термин употребил в 1202 году первый крупный математик средневековой Европы Леонардо Пизанский (1170 - 1250), более известный как Фибоначчи. Полноценная теория обыкновенных дробей и операций над ними сложилась в XVI веке в работах итальянского математика Никколо Тартальи (1499 - 1557) и немецкого и итальянского математика, астронома Христофора Клавиуса (Клавия) (1537 - 1612). В древней Руси дроби называли долями или ломаными числами. Русский термин "дробь" происходит от латинского слова "fractura", которое в переводе с арабского означает "ломать", "раздроблять". Термин "дробь" используется в "Арифметике" русского математика и педагога Леонтия Филипповича Магницкого (1669 - 1739) как для обыкновенных, так и для десятичных дробей.
Десятичные дроби впервые встречаются в Китае примерно с III века н.э. при вычислениях на счётной доске. В Европе же впервые десятичные дроби применяет еврейский математик и астроном Иммануил Бонфис бен Яаков (1300 - 1377) около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина "Десятая" (1585).