1. записать бесконечно периодическую дробь в виде обыкновенной дроби:
1). 0,(5) 2).2,6(3)
2. докажите, что прогрессия бесконечно убывающая:
1). 7; 1; 1/7 2). -0,2; 0,04; -0,008
3. найдите сумму бесконечно убывающей прогрессии:
1). 0,6; 0,006; 0,0006
2).1/4; -1/16; 1/64
4. выяснить, является ли бесконечно убывающей прогрессией последовательность заданная формулой н-ого члена:
bn=3^n-1*7^2-n
 книги
книги 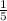 книги
книги =
= 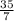 = 5 (руб.) - стоит ручка
= 5 (руб.) - стоит ручка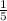 =
= 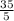 = 7 (руб.) - стоит тетрадь
= 7 (руб.) - стоит тетрадь =
= 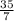 = 5 (руб.) - стоит ручка
= 5 (руб.) - стоит ручка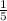 =
= 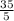 = 7 (руб.) - стоит тетрадь
= 7 (руб.) - стоит тетрадь
Числа можно округлять до десятых, сотых, тысячных и так далее. Записывают результат округления после специального знака «≈». Этот знак читается как «приближённо равно».
Если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется (12,33 ~ 12,3)
Если первая из отбрасываемых цифр (считая слева направо) равна или больше 5 без предшествующего округления, то последняя сохраняемая цифра увеличивается на единицу (0,145 ~ 0,15; 0,156 ~ 0,16)
Если первая из отбрасываемых цифр (считая слева направо) равна 5, но получена в результате предшествующего округления в большую сторону, то последняя сохраняемая цифра не меняется (0,25 ~ 0,2, т. к. 0,25 получено из 0,248), а при предшествующем округлении в меньшую сторону последняя сохраняемая цифра увеличивается на единицу (0,25 ~ 0,3, т. к. 0,25 получено из 0,252).