Пошаговое объяснение:
Дана функция y=(x-8)²·(x-9)+1 на отрезке [-4; 8,5].
Находим производную от функции:
y' = ((x-8)²·(x-9)+1)' = ((x-8)²)'·(x-9)+(x-8)²·(x-9)'+0 = 2·(x-8)·(x-9)+(x-8)² =
= 2·x²-34·x+144+x²-16·x+64 = 3·x²-50·x+208.
Определим стационарные точки:
y' = 0 ⇔ 3·x²-50·x+208=0. Тогда
D = (-50)²-4·3·208 = 2500-2496 = 4 = 2²,
x₁=(50-2)/(2·3)=48/6=8∈[-4; 8,5],
x₂=(50+2)/(2·3)=52/6=8 4/6=8 2/3 ∉[-4; 8,5].
Вычислим значения функции при x = -4, x = 8 и x = 8,5:
y(-4) = (-4-8)²·(-4-9)+1 = 144·(-13)+1 = -1872+1 = -1871;
y(8) = (8-8)²·(8-9)+1 = 0·(-1)+1 = 0+1 = 1;
y(8,5) = (8,5-8)²·(8,5-9)+1 = 0,25·(-0,5)+1 = -0,125+1 = 0,875.
Наибольшее значение функции y=(x-8)²·(x-9)+1 на отрезке [-4; 8,5] :
y(8) = 1.
-15
Пошаговое объяснение:
Чтобы найти сумму целых решений неравенства, удовлетворяющих условию, составим систему неравенств и решим её.
ОДЗ x≤12
решим первое неравенство
1 случай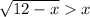 
при х≥0
x∈(-4;3), но при х≥0 ⇒x∈[0;3)
2 случай 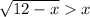при х<0
x∈R, но при при х<0 ⇒ x∈(-∞;0)
общее решение x∈(-∞;3)
решим второе неравенство
1 случай x<7 при х≥0 х∈[0;7)
2 случай -х<7, при х<0 х∈(-7;0)
общее решение x∈(-7;7)
найдем пересечение обоих решений и проверим ОДЗ x≤12
х∈(-7; 3)
Целые решения из полученного промежутка складываем и находим сумму: -6-5-4-3-2-1+0+1+2= -18
2) 20:250=2/25 -части сплава составляет медь