Первое число 60. второе число состовляет 80% первого , а третье число состовляет 50% суммы первого и второго. найдите среднее арифметическое этих чисел

👇

Увидеть ответ

Ответ:

Dianissimolps

11.08.2020

1-е число = 60

2-е число =80% от 60

Пропорция:

60 - 100%

х - 80%, отсюда х = 60*80 / 100 = 48

2-е число = 48

Вычислим 3-е число: 50% от (60+48)

108 - 100 %

х - 50%, отсюда х = 108*50 / 100 = 54

Теперь вычислим ср.арифметическое: (60 + 48 + 54 ) / 3 = 54

4,5(23 оценок)

Ответ:

Флаксария

11.08.2020

60*80%=48 60+48=108 108*50%=54 108+54=162 162:3=54

4,7(59 оценок)

Открыть все ответы

Ответ:

kotelnikovaLA

11.08.2020

Чтобы определить координатный луч, нам сначала потребуется, конечно же, сам луч. Итак, построим луч, обозначим его OX, точка O – начало луча. Забегая вперед, скажем, что точку O называют началом отсчета координатного луча. Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала. Так у нас есть луч. Как же его сделать координатным лучом? Во-первых, над точкой O нужно написать число 0. Во-вторых, нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1. В-третьих, на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному, далее от конца этого отрезка нужно отложить еще один единичный отрезок, от конца построенного отрезка нужно отложить еще один единичный отрезок, и так далее. Наконец, чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2, 3, 4, … Так координатный луч представляет собой не что иное, как бесконечную шкалу. Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа 0 и 1. Этот вариант изображения координатного луча приведен на рисунке ниже. В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче. Также допускается буквы O и X записывать над лучом, а числа – под лучом. Наконец, не удивляйтесь, если в обозначении координатного луча Вы увидите одновременно и маленькую и большую буквы. Наиболее часто придется сталкиваться с координатными лучами, обозначенными как Ox, Oy и Oz.

4,4(30 оценок)

Ответ:

sergejryazanov228

11.08.2020

1.
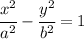Уравнение гиперболы имеет стандартный вид: $\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1$ , где а и b - полуоси гиперболы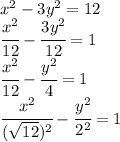
$x^2-3y^2=12 
\\\
 \cfrac{x^2}{12} - \cfrac{3y^2}{12} =1
\\\
 \cfrac{x^2}{12} - \cfrac{y^2}{4} =1
\\\
 \cfrac{x^2}{( \sqrt{12} )^2} - \cfrac{y^2}{2^2} =1$
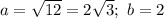
Значит, у гиперболы $a= \sqrt{12} =2 \sqrt{3} ;\ b=2$
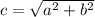
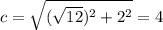
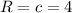
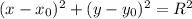Правый фокус гиперболы имеет вид F(c; 0), где $c= \sqrt{a^2+b^2}$
Находим с:
$c= \sqrt{( \sqrt{12})^2+2^2 } =4$
Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть R=c=4

Общий вид уравнения окружности: (x-x_0)^2+(y-y_0)^2=R^2

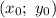, где $(x_0; \ y_0)$ - центр окружности, R - ее радиус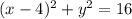
Уравнение окружности: (x-4)^2+y^2=16

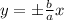
Асимптоты гиперболы имеют вид: $y=\pm \frac{b}{a} x$
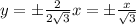
Тогда, асимптоты гиперболы $y=\pm \frac{2}{2 \sqrt{3} } x=\pm\frac{ x }{\sqrt{3}}$
Подставляем в уравнение окружности выражение для у:
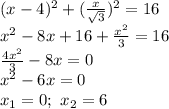
$(x-4)^2+( \frac{x}{ \sqrt{3} } )^2=16
\\\
x^2-8x+16+ \frac{x^2}{ 3} } =16
\\\
 \frac{4x^2}{ 3} }-8x =0
\\\
x^2-6x =0
\\\
x_1=0; \ x_2=6$
Тогда у для соответствующих х равны:
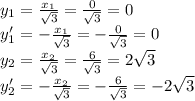
$y_1= \frac{x_1}{ \sqrt{3} } =\frac{0}{ \sqrt{3} } =0 \\\ y_1'= -\frac{x_1}{ \sqrt{3} } =-\frac{0}{ \sqrt{3} } =0 \\\ y_2= \frac{x_2}{ \sqrt{3} } =\frac{6}{ \sqrt{3} } =2 \sqrt{3} 
\\\
y_2'= -\frac{x_2}{ \sqrt{3} } =-\frac{6}{ \sqrt{3} } =-2 \sqrt{3}$
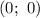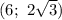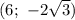
ответ: $(0; \ 0)$ ; $(6; \ 2 \sqrt{3} )$ ; $(6; \ -2 \sqrt{3} )$

2.
Так как известна одна полуось и точка, принадлежащая гиперболе, о можно найти вторую полуось:
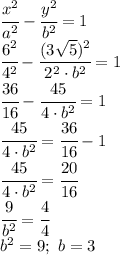
$\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2} =1
\\\
 \cfrac{6^2}{4^2} - \cfrac{(3 \sqrt{5}) ^2}{2^2\cdot b^2} =1
\\\
 \cfrac{36}{16} - \cfrac{45}{4\cdot b^2} =1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{36}{16}-1
\\\
 \cfrac{45}{4\cdot b^2} = \cfrac{20}{16}
\\\
 \cfrac{9}{b^2} = \cfrac{4}{4}
\\\
b^2=9; \ b=3$
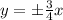
Тогда уравнения асимптот принимают вид: $y=\pm \frac{3}{4} x$
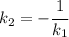
Угловой коэффициент перпендикулярной прямой является обратным и противоположным числом к угловому коэффициенту исходной прямой: $k_2=- \cfrac{1}{k_1}$
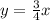Тогда, для прямой $y=\frac{3}{4}x$ таким коэффициентом является число 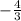$- \frac{4}{3}$ , а для прямой 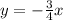$y=-\frac{3}{4}x$ - число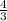 $\frac{4}{3}$
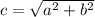
Левый фокус гиперболы имеет вид F(-c; 0), где $c= \sqrt{a^2+b^2}$
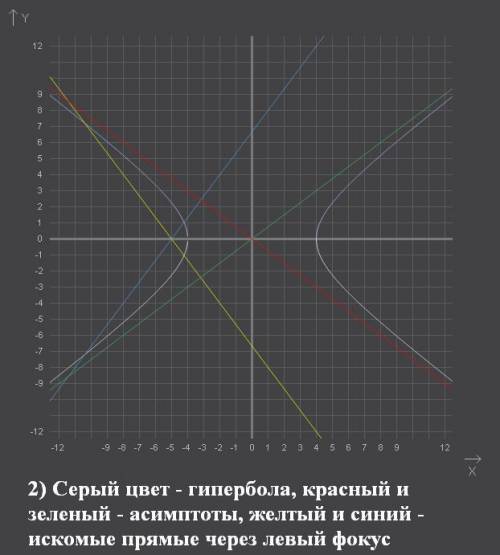
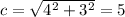$c=\sqrt{4^2+3^2} =5$ , следовательно через точку (-5; 0) нужно провести искомые прямые
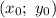Уравнение прямой, проходящей через заданную точку $(x_0; \ y_0)$ с заданным угловым коэффициентом k имеет вид: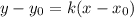 y-y_0=k(x-x_0)

Тогда:
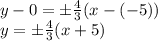
$y-0=\pm \frac{4}{3} (x-(-5))
\\\
y=\pm \frac{4}{3} (x+5)$
Или по отдельности:
$y_1=\frac{4}{3} (x+5)=\frac{4}{3} x+ \frac{20}{3} 
\\\
y_2=-\frac{4}{3} (x+5)=-\frac{4}{3} x- \frac{20}{3}$

№1. найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе