Пошаговое объяснение:
Чисто технически:
1) за 1000 дней вырастет 1000*(1000/100) = 1000*10 = 10 000кг травы
2) 2 пары овец съедят (за 1000 дней): 2*2*2*1000 = 8 000кг
а пара коров: 2*4*1000 = 8 000кг
то есть будет съедено: 8 000 + 8 000 = 16 000кг травы
3) 10 000 - 16 000 = -6 000
Это означает, что на луге травы станет на 6 000 кг меньше, чем было до того, как стали выпускать на луг скот.
То, сколько травы осталось сосчитать нельзя, так как не дано начальное ее количество.
Надеюсь, мой ответ хоть что-то пояснил))
1) 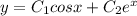
2) 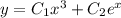
Пошаговое объяснение:
ЛОДУ 2ого порядка с переменными коэффициентами имеет вид 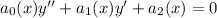
Общее решение такого ДУ - линейная комбинация двух его линейно независимых частных решений.
В обоих заданиях необходимо заметить, что сумма коэффициентов 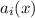 равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция
равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция 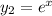 [и действительно:
[и действительно: 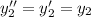 , а тогда уравнение принимает вид
, а тогда уравнение принимает вид 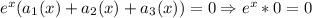 - верное равенство].
- верное равенство].
1) Рассмотрим Вронскиан системы 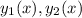 :
:
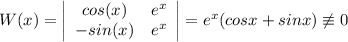
Значит, данные частные решения линейно независимы - а тогда общее решение имеет вид 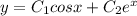 .
.
2) Очевидно искать частное решение в виде многочлена. Пусть его старший член равен  [коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е.
[коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е.  .
.
Тогда
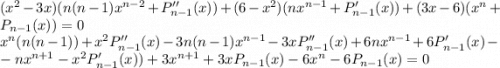
То есть коэффициент при старшей степени 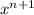 получаемого в левой части многочлена равен
получаемого в левой части многочлена равен  [степень
[степень 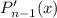 не выше
не выше 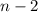 , а
, а 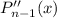 не выше
не выше 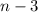 ]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
Нетрудной подстановкой 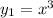 убеждаемся, что это решение ДУ:
убеждаемся, что это решение ДУ:
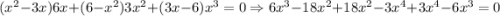 - верное равенство.
- верное равенство.
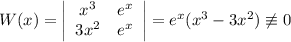
А тогда общее решение имеет вид
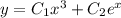
Общая скорость катеров: 20 + 25 = 45 км/час. Следовательно, до встречи 1-го катера со вторым ч.