Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
15 = 3 · 5
18 = 2 · 3 · 3
Общие множители чисел: 3
НОД (15; 18) = 3
Наименьшее общее кратное::
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.
18 = 2 · 3 · 3
15 = 3 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (15; 18) = 2 · 3 · 3 · 5 = 90
Наибольший общий делитель НОД (15; 18) = 3
Наименьшее общее кратное НОК (15; 18) = 90
Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
600 = 2 · 2 · 2 · 3 · 5 · 5
1075 = 5 · 5 · 43
Общие множители чисел: 5; 5
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (600; 1075) = 5 · 5 = 25
Наименьшее общее кратное::
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.
1075 = 5 · 5 · 43
600 = 2 · 2 · 2 · 3 · 5 · 5
Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:
НОК (600; 1075) = 5 · 5 · 43 · 2 · 2 · 2 · 3 = 25800
Наибольший общий делитель НОД (600; 1075) = 25
Наименьшее общее кратное НОК (600; 1075) = 25800
Пошаговое объяснение:
1. б) (-3; 8]
2. а)
3. x∈ [-1; 2)
4. x∈ (-3; +∞)
5. x∈ (-1,5; 6]
6. x∈ [1/5; 2]
7. x∈ (-∞; 12]
8. x∈ [-2; 3]
Пошаговое объяснение:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3. 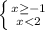
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4. 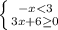

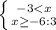
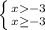
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
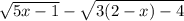
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:

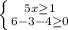


1/5 ≤ x ≤ 2 или x∈ [1/5; 2]
7. Решите совокупность неравенств
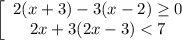
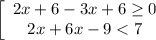
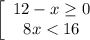

Отсюда х ≤ 12 или x∈ (-∞; 12]
8. 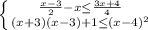
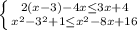

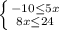

Отсюда -2 ≤ х ≤ 3 или x∈ [-2; 3]
140-15=125 яблок было в корзине