Дроби приводятся к одному знаменателю, числители складываются
Например:
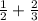приводим к общему знаменателю 6, умножая первую дробь на 3, вторую на 2, получаем: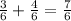 
Десятичные числа:
те же дроби в виде десятичного числа:
0,5+0,66=1,16
2) Вычитание проводим аналогичным , как и сложение
3) Умножениечислитель умножается на числитель, знаменатель на знаменатель
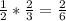
переворачиваем дробь и умножаем
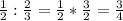
Дроби: числитель в степень, знаменатель в степень
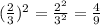
Десятичные числа: не обращаем внимания на ноль, возводим в степень после запятой
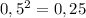
(-+) означает, что ставится знак того числа, которое по модулю больше
Например: (-)8+(+)13=(+)5
(+)20-40=(-)20
Не имеет значения, какое число первое, отрицательное или положительное, результат тот же, что в правиле
(-)*(+)=(-) и так же (+)*(-)=(-)
Все действия аналогично
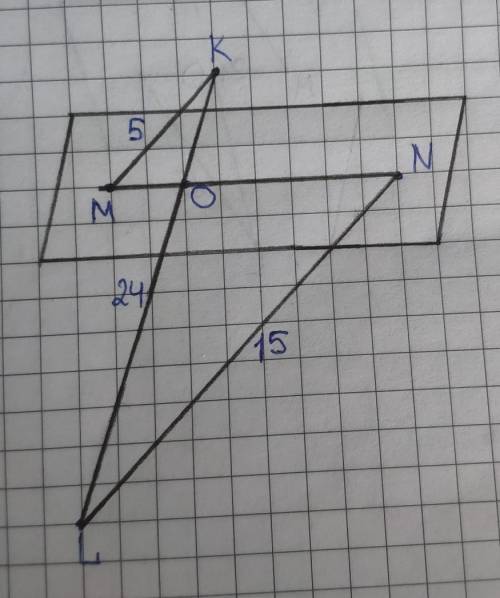
Две прямые в пространстве паралельны если они лежат на одной плоскости и не пересекаются.
Так как MK||NL, то они лежат на одной плоскости, пусть эта плоскость – плоскость а.
Так как точки M, K, N, L принадлежат плоскости а, то прямые KL u MN так же лежат на ней.
Рассмотрим ∆MOK и ∆NOL.
KL=24 дм по условию, пусть КО=х дм, тогда LO=24–x.
Угол MOK=угол NOK как вертикальные,
Угол MKL=угол NLK как накрест-лежащие при параллельных прямых MK и NL и секущей KL.
Тогда ∆MOK~∆NOK по двум равным углам.
Стороны подобных треугольников пропорциональны.
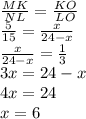
То есть KO=6 дм, LO=24–6=18 дм.
ответ: 6 дм, 18 дм.
P=(a+b)*2=(11+6)*2=34(см)