1. AC = 12
2. BD = 2
3. DC= 4; AC =16; AB=4 \sqrt{12}
Пошаговое объяснение:
1. DE треугольника DBE находится по теореме Пифагора: 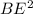 =
= 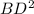 +
+ 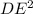 , где DE=
, где DE= 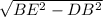
Так как DE = средняя линия треугольника ABC (AD = DB) то AC = 2DE. Отсюда, AC= 12
2. AC находится по той же теореме Пифагора: AC =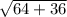 =10
=10
BD = медиана треугольника ABC, так как она делит AC на равные отрезки, тогда
BD =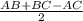 = (6+8-10)/2 =2
= (6+8-10)/2 =2
3. DC= 4 - показано на рисунке.
Так как угол DBC треугольника BDC равен 30 градусам, то гипотенуза этого треугольника будет равна 8, потому что катет, лежащий против угла в 30 градусов в прямоугольном треугольнике равен половине гипотенузы. Значит BC = 8.
Если угол DBC = 30 градусов, то смежный ему угол DBA= 60 градусов, так как угол ABC = 90 градусов. Теперь рассмотрим прямоугольный треугольник ADB. Если угол DBA = 60 градусов, то угол BAD = 30 градусов. Так как угол BAD =30 граудсов, то BC = 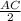 . Получается, что AC = 16. Для нахождения AB применим теорему Пифагора: AB =
. Получается, что AC = 16. Для нахождения AB применим теорему Пифагора: AB =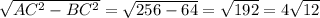
1 Задача:
V1=95км/ч, V2=4/5км от 95км/ч, t=3ч, S=15км
1) Узнаем скорость второго катера:
4/5 из 95 км/ч=95:5*4=76км/ч
2) Узнаем скорость удаление:
Vуд=V1+V2
Vуд=95км/ч+76км/ч=171км/ч
3)Узнаем расстояние между катерами через 3 часа:
171км/ч*3ч=513км
513км+15км=528км
ответ: Расстояние между катерами через 3 часа будет 528 км.
2 Задача:
V1=84км/ч, V2=5/6км/ч от 84 км/ч, t=4ч, S=26км
1) Узнаем скорость второго поезда:
5/6 от 84км/ч=84:6*5=70км/ч
2) Скорость сближение:
Vсбл=V1+V2
Vсбл=84км/ч+70км/ч=154км/ч
3) Расстояния между поездами через 4часа:
154км/ч*4ч=616км
4) Расстояние между городами:
616км+26км=642км
ответ: Расстояние между городами 642км.
Y=(x+4)²/(x-5)
ИССЛЕДОВАНИЕ
1.Область определения D(x) -в знаменателе - х-5≠0 и х≠5.
Х∈(-∞;5)∪(5;+∞). Вертикальная асимптота: х = 5
2. Пересечение с осью Х. Y=(x+4)=0 при х =-4.
3. Пересечение с осью У. У(0) = -16/5 = - 3.2.
4. Поведение на бесконечности и в точке разрыва.
Y(x)= (x²+ 8x+16)/(x-5), Y(x)/x = (x+8+ 16/x)/(1-5/x)
.limY(-∞) = - ∞ limY(+∞) = +∞, lim(5-)= -∞, lim(5+)=+∞.
5. Исследование на чётность.Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= x².??????????????
Корни при Х1=0. Схема знаков производной.
(-∞)__(>0)__(-4)___(<0)___(14)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(-4)= 0, минимум – Ymin(14)=36.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-4)∪(14;+∞) , убывает = Х∈(-4;5)∪ (5;14).
8. Вторая производная - Y"(x) = 2x=0.
Корень производной -
Точка перегиба Y"(x)= 0 совпадает с точкой разрыва х = 5.
9. Выпуклая “горка» Х∈(-∞;5), Вогнутая – «ложка» Х∈(5;+∞).
10. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
k=lim(∞)Y(x)/x = х
b = lim(∞)Y(x) – k*x = 13 (???)
11. График в приложении.