84
Пошаговое объяснение:
Треугольник является прямоугольным, значит, у него два катета a и b, гипотенуза c. По условию одна из сторон 12 (единицу можно выбрать произвольное). Эта сторона будет катетом, в противном случае, если эта сторона гипотенуза c, то из-за ограничения для катетов a<c и b<c максимально возможный периметр также ограничивается. Поэтому наименьший катет, пусть этот катет будет a, выберем как a=12.
Так как треугольник прямоугольный, то верна теорема Пифагора
c² = a² + b² или c² - b²= 12² или (c - b)·(c + b)= 144.
С другой стороны, из условия существования треугольника (другое название - неравенство треугольника) получаем
a + c > b
b + c > a
a + b > c
Из последнего неравенства вытекает, что 12 > c - b.
Теперь рассмотрим (c - b)·(c + b)= 144. Из того, что длины сторон треугольника являются целыми числами (вообще то натуральными числами), то (c - b) и (c + b) также являются натуральными числами.
Обозначим c - b = х. Отсюда c = x + b. Тогда
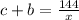
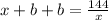
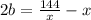
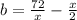
Отсюда следует, что х - чётное и является делителем 72.
Учитывая 12 > c - b и то, что чем меньше c - b, тем больше периметр, рассмотрим разложение числа 144 на чётные множители: 144=2·72.
Тогда c - b = 2 и c + b = 72. Отсюда c = 37 и b = 35. Ясно, что неравенство треугольника выполняется, оба числа целые.
Проверим утверждение теоремы Пифагора:
12²+35²=144+1225=1369=37².
Значит, все условия выполняются. Тогда максимально возможный периметр равен сумме длин сторон треугольника
P = a + b + c = 12 + 35 + 37 = 84
Пошаговое объяснение:
Левая чашка 3 пачки +0,5 кг
Правая чашка - 1 пачка + 3 кг
Весы находятся в равновесии.
Решение.
1) х кг - масса 1 пачки сахара.
Составим уравнение:
3х+0,5=х+3;
3x-x=3-0.5;
2x=2.5
x= 1.25 кг - масса 1 пачки сахара.
***
2) х книг во втором шкафу.
в первом - 4х книг.
из 1 шкафа забрали 25 книг -- осталось 4х-25 книг.
во 2 шкаф положили 17 книг -- стало х+17 книг.
4х-25=х+17;
4x-x=17+25;
3x=42;
x=14 книг было во 2 шкафу.
Проверим:
4*14 = 56 книг в 1 шкафу.
14 книг во 2 шкафу.
56-25 = 14+17;
31=31. Всё верно!
=2 1/2
V=2,5 см3