integral 1/(sqrt(9-x^2) (x^2+16)) dx
For the integrand 1/(sqrt(9-x^2) (x^2+16)), Сделаем подстановку x = 3sin(u), тогда dx = 3cos(u)du. Отсюда sqrt(9-x^2) = sqrt(9-9sin^2(u)) = 3cos(u), u =arcsin(x/3), получаем:
= integral du/(9 sin^2(u)+16)
1/(9 sin^2(u)+16) числитель и знаменатель разделим на cos^2(u):
integral (du/cos^2(u))/(9 tg^2(u)+16/cos^2(u))
Т.к. 1/cos^2(u) = tan^2(u)+1:
integral (du/cos^2(u))/(25tg^2(u)+16)
Сделаем подстановку s = tg(u) тогда ds = du/cos^2(u) :
= integral ds/(25s^2+16)
= integral ds/(16 [(25s^2)/16+1])
Выносим константу:
= 1/16 integral ds/[(25s^2)/16+1]
Подстановка p = (5 s)/4 и dp = 5/4 ds:
= 1/20 integral dp/(p^2+1)
integral ds/(p^2+1) = arctg(p):
= 1/20 arctg(p)+C
Возвращаенмся к заменам: для p = (5 s)/4:
= 1/20 arctg((5 s)/4)+C;
для s = tg(u):
= 1/20 arctg((5 tg(u))/4)+C;
для u = arcsin(x/3):
1/20 arctg((5 tg(arcsin(x/3)))/4)+C
tg(arcsin(x/3)=x/(3 sqrt(1-x^2/9))
Answer:
= 1/20 arctg((5x)/[4 sqrt(9-x^2)])+C
когда находим производную такого вида а^x, где а-некая константа, в нашем случае а=2;
вычисляется она (a^x)'=(a^x)*ln a=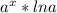
. Выводится это по определению, через пределы.
а теперь ближе к примеру:
1)производная суммы = сумме призводных
(2^x + 2^(2-x))'= (2^x)' + (x^(2-x))'
2) (2^x)'=(2^x) * ln2
мы видим, что второе слогаемое имеет в степени не просто х, а 2-х - это уже сложная функция и будем искать производную по правилам поиска производной от сложной функции, а именно
3) (2^(2-x))'=(2^(2-x))*ln2*(2-x)'=(2^(2-x))*ln2*(0-1)= - (2^(2-x))*ln2
пояснение: (2-x)'= (2)'-(x)'=0-1
4) (2^x + 2^(2-x))'= (2^x) * ln2 - (2^(2-x))*ln2 =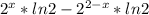 
- это и есть ответ можно для красоты лагорифм 2 вынести за скобки но особой роли это не сыиграет
