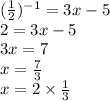
Пошаговое объяснение:
Множества A и B называются равными, если они состоят из одних и тех же элементов, причем порядок элементов в множествах не существенен. Иными словами, если каждый элемент множества
A является также элементом множества B
, и каждый элемент множества B является также элементом множества A, то A=B
В нашем случае равные множества :
1) B1 = {15; 21; 4; 7} ; B4 = {4; 21; 7; 15}; B3 = {21; 7, 15, 4,}; значит
В1=В3=В4
2) B6 = {Всё буквы русского алфавита, n, o, y}; B9 = {Всё буквы кыргызского алфавита}.
Кыргызский алфавит содержит все буквы русского алфавита и n, o, y, значит :
В6= В9
Сумма двух простых восьмизначных уже составное, т.к. независимо, от того, каким оно было исходным, в сумме двух нечетных результат будет четным, а, значит, оно будет делиться на 2, кроме того, на себя и единицу, т.е. и будет составным. Что касаемо четных простых, то это число только равно 2 и не является восьмизначным. Условие не является необходимым, т.к. если сумма двух натуральных есть составное, оно не обязательно будет восьмизначным. Пример из того, что 7+11=18 не следует, что 7 и 11-восьмизначные.