1)
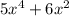
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
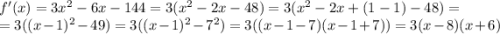
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
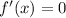
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
Чтобы успешно использовать на практике операцию извлечения корня, нужно познакомиться со свойствами этой операции, что мы и сделаем настоящем параграфе.
Все свойства формулируются и доказываются только для неотрицательных значений переменных, содержащихся под знаками корней.
Доказательство. Введем следующие обозначения: Нам надо доказать, что для неотрицательных чисел х, у, z выполняется равенство х-уz.
Так как
Итак, Но если степени двух неотрицательных чисел равны и показатели степеней равны, то равны и основания степеней; значит, из равенства xn =(уz)п следует, что х-уz, а это и требовалось доказать.
Приведем краткую запись доказательства теоремы.
Замечания:
1. Теорема 1 остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.
2. Теорему 1 можно сформулировать, используя конструкцию "если...то» (как это принято для теорем в математике). Приведем соответствующую формулировку: если а иb — неотрицательные числа, то справедливо равенство Следующую теорему мы именно так и оформим.
Краткая (хотя и неточная) формулировка, которую удобнее использовать на практике: корень из дроби равен дроби от корней.
Доказательство. Приведем краткую запись доказательства теоремы 2, а вы попробуйте сделать соответствующие комментарии, аналогичные тем, что были приведены при доказательстве теоремы 1.конечно, обратили внимание на то, что доказанные два свойства корней п-й степени представляют собой обобщение известных вам из курса алгебры 8-го класса свойств квадратных корней. И если бы других свойств корней п-й степени не было, то как бы все было просто (и не очень интересно). На самом деле есть еще несколько интересных и важных свойств, которые мы обсудим в этом параграфе. Но сначала рассмотрим несколько примеров на использование теорем 1 и 2.
Пример 1. Вычислить
Решение. Воспользовавшись первым свойством корней (теорема 1), получим:
Замечание 3. Можно, конечно, этот пример решить по-другому, особенно если у вас под рукой есть микрокалькулятор: перемножить числа 125, 64 и27,а затем извлечь кубический корень из полученного произведения. Но, согласитесь, предложенное решение «интеллигентнее».
Пример 2. Вычислить
Решение. Обратим смешанное число в неправильную дробь.
Имеем Воспользовавшись вторым свойством корней (теорема 2), получим:
Пример 3. Вычислить:
Решение. Любая формула в алгебре, как вам хорошо известно, используется не только «слева направо», но и «справа налево». Так, первое свойство корней означает, что можно представить в виде , наоборот, можно заменить выражением . То же относится и ко второму свойству корней. Учитывая это, выполним вычисления:
Пример 4. Выполнить действия:
Решение, а) Имеем:
б) Теорема 1 позволяет нам перемножать только корни одинаковой степени, т.е. только корни с одинаковым показателем. Здесь же предлагается умножить корень 2-й степени из числа а на корень 3-й степени из того же числа. Как это делать, мы пока не знаем. Вернемся к этой проблеме позднее.
Продолжим изучение свойств радикалов.
Иными словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Это — следствие теоремы 1. В самом деле, например, для к = 3