- это та часть поля, которую вспахивает 1-ый тракторист за 1 день, а 
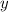- та часть поля, которую вспахивает уже 2-ой тракторист, но тоже за 1 день.Мы можем составить систему уравнений!
За 4 дня первый тракторист вспашет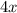
части поля, а второй - 
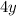части поля. И, по условию, сумма этих двух чисел равна 1 (полю).Время, за которое 1-ый трактор вспашет 
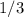поля составляет 
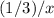, а то время, за которое второй трактор вспашет 
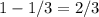поля равно не иначе, как 
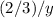. И сумма этих двух отрезков времени - 10 дней.Есть две переменных - но и есть два уравнения:
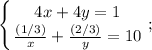
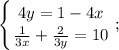
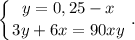
Можем сделать подстановку:
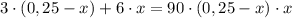
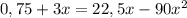
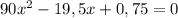
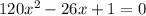
Дальше, воспользовавшись формулой корней полного квадратного уравнения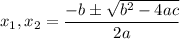 
, получим:
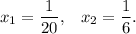
Осталось только 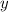-и найти:
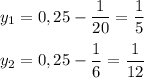
Итак, у нас есть два решения, и между ними придется сделать выбор.
По условию дано, что " ... первый работает медленнее ... ". Это означает, что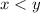 
.
Но под этот критерий подходит только первое решение (так как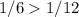 
):
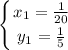
Если мы сделаем проверку, то это решение будет удовлетворять всем условиям.
Но все же заметим, что пока ответа задачи у нас нет. Так что самое время его получить.
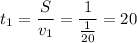(дней)
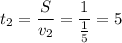(дней)
Задача [наконец] решена!
ответ:первый тракторист может вспахать поле за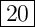 
дней,
а второй - за 
дней.
След секущей плоскости в основании - это хорда, отстоящая от центра на величину b. Длину её примем равной а.
Проведём дополнительное осевое сечение перпендикулярно хорде а.
В сечении - прямоугольный равнобедренный треугольник с острыми углами по 45 градусов, с катетами L, с основанием 2r.
Заданная секущая плоскость(это равнобедренный треугольник)
рассечётся по высоте этого треугольника и с осью конуса образует прямоугольный треугольник с острыми углами в 60 градусов у основания и 30 градусов у оси.
Величина b равна:
b = r/tg 60° = r/√3 = r√3/3.
Отсюда находим длину хорды а:
а = 2√(r² - b²) = 2√(r² - (r²/3)) = 2√(2r²/3) = 2r√(2/3).
Высота h треугольника сечения как гипотенуза в треугольнике с углом 30 градусов равна: h = 2b = 2r√3/3.
Площадь S сечения как треугольника с основанием а и высотой h равна:
S = (1/2)ah = (1/2)*(2r√(2/3))*(2r√3/3) = (2√6)r²/9.