Пошаговое объяснение:
В №1 надо вычислить определитель матрицы 4х4, каждый элемент которого равен х (определитель равен 0, т.к. есть две одинаковые строки).
В №2 надо найти произведение двух матриц А (2х3) и В (3х1) - матрицу С размером 2х1 (столбец из двух чисел - 3 и 3).
В №3 судя по всему решить систему методом Крамера (с параметрами а, е, с), хотя очевидно, что решений нет - 3 одинаковых суммы равны 3 разным числам. Методом Крамера получится, что определитель матрицы коэффициентов равен нулю, т.к. есть одинаковые строки, что, по правилу Крамера, равнозначно несовместности системы.
Если исключить возможность выбора одного и того же человека дважды, то всего можно выделить 52*51=2652 различных пар людей.
1) Оба имеют фамилию, начинающуюся с согласной. Для получения этого исхода изначально есть возможность выбрать одного из 37 человек, а затем выбрать еще одного из 36 оставшихся.
Тогда всего вариантов 37*36=1332
И вероятность 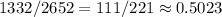
2) Первый имеет согласную, другой гласную (или обратная ситуация, отсюда умножение на 2): 37*15*2=1110
Вероятность: 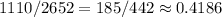
3) Хотя бы один имеет фамилию, нач. с гласной... Т.е. оба имеет такую фамилию или только один; запрещена ситуация, когда оба имеют фамилии нач. с согласных (1-ый случай), отсюда вероятность:
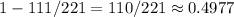
50:6=8(ост.2)
502:11=45(ост.7)
1132:104=10(ост.92)