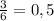, следовательно вероятность того, что выпадет число, которое не больше 3, тоже равна 0,5, то есть при одном бросании кубика с одной и той же вероятностью реализуется либо событие 1 (выпало число больше 3), либо событие 2 (выпало число не больше 3). Отсюда можно сделать вывод, что при двух бросках может быть 4 события: 1-1, 1-2, 2-1, 2-2. Нам же нужно первое событие. Тогда вероятность того, что выпадет число, больше трех, равна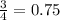 
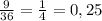
Всех возможных вариантов, что будут только задания, которые решал ученик:
6 * 5 * 4 * 3 * 2
То есть вероятность, что будут только задания, которые он решал:
Р(А) = 6 * 5 * 4 * 3 * 2/10 * 9 * 8 * 7 * 6 = 1/42
Вероятность обратного равна 1 - 1/42 = 41/42
ответ: 41/42