Длина прямоугольного параллелепипеда равна 6см,ширина-5 см,высота-7 см.длина ребра куба составляет 6 см.что больше: объем прямоугольного параллелепипеда или объем куба? и на сколько?

👇

Ответ:

Alex1t0

26.05.2021

Объем параллелепипеда: 6 * 5 * 7 = 210 см³
Объем куба: 6 * 6 * 6 = 216 см³
216 > 210, то есть объем куба больше
216 - 210 = 6(см³) - больше объема параллелепипеда
ответ: больше на 6 см³.

4,6(54 оценок)

Открыть все ответы

Ответ:

tatiana2017D

26.05.2021

1. 7х+20=5х-2

7х-5х=-20-2

2х=-22

х=-11

2. 11х+7=6х-19

11х-6х=-7-19

17х=-26

х=-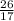 $\frac{26}{17}$

х=-1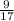 $\frac{9}{17}$

3. 9-3х=х+20

-3х-х=-9+20

-4х=-11

х=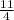 $\frac{11}{4}$

х=2,75

4. 0,2х+2,7=1,4-1,1х

0,2х+1,1х=-2,7+1,4

1,3х=-1,3

х=-1

5. 3,7х-0,7=4,2+1,2х

3,7х-1,2х=0,7+4,2

2,5х=4,9

х=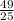 $\frac{49}{25}$

х=1,96

6. 5,36х-0,3=0,2-0,64х

5,36х+0,64х=-0,3+0,2

6х=-0,5

х=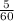 $\frac{5}{60}$

х=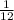 $\frac{1}{12}$

7. 5(х-4)=х+8

5х-20=х+8

5х-х=20+8

4х=28

х=7

8. 2(6х+7)=19+14х

12х+14=19+14х

12х-14х=-14+19

-2х=-5

х=2,5

9. 5(1-х)=2(х-8)

5-5х=2х-16

-5х-2х=-5-16

-7х=-21

х=3

10. 0,2(3х-4)=1,6(х-2)

0,6х-0,8=1,6х-3,2

0,6х-1,6х=0,8-3,2

-х=-2,4

х=2,4

11. 8(2х+1)+1=3(4х-2)-1

16х+8+1=12х-6-1

16х-12х=-8-1-6-1

4х=-16

х=-4

12. 0,3(8-3х)=3,2-0,8(х-7)

2,4-0,9х=3,2-0,8х+5,6

-0,9х+0,8х=-2,4+3,2+5,6

-0,1х=6,4

-х=64

х=-64

4,8(96 оценок)

Ответ:

REDbad5

26.05.2021

1) Рассмотрим квадрат. Пусть в его вершинах стоят числа 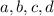a,b,c,d (см.рис.)

Для любого такого квадрата введем величину: 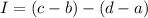I=(c-b)-(d-a) . Видно, что она постоянна при указанных действиях (добавление 1 к числам на ребре).

2) Очевидно, что последовательность действий не влияет на конечный результат. Поэтому пусть сначала действия производятся внутри верхних и нижних квадратов, а затем на ребрах (в данном случае вертикальных), которые эти квадраты соединяют. Пусть нам удалось получить куб с 8 равными числами. Пусть были сделаны все действия в квадратах. Тогда числа на вертикальных ребрах равны — иначе их не уравнять (мы сохраняем разность чисел). Если все числа на ребрах равны, то достаточно просто применить нужное количество операций к этим ребрам, чтобы получить все равные числа. Итак, наша задача имеет решение тогда и только тогда, когда один квадрат возможно перевести в другой. А эта задача, в свою очередь, имеет решение тогда и только тогда, когда величина 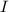для них совпадает.

3) Рассматриваем первый куб: верхний квадрат: 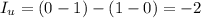$I_{u}=(0-1)-(1-0)=-2$ , нижний 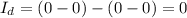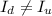$I_{d}=(0-0)-(0-0)=0$ , $I_{d}\neq I_{u}$ — задача решения не имеет.

Второй: верхний квадрат 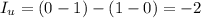$I_{u}=(0-1)-(1-0)=-2$ , нижний — 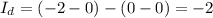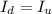$I_{d}=(-2-0)-(0-0)=-2$ ; $I_{d}=I_{u}$ — задача имеет решение. Привести пример просто. Вот на словах: применяем операцию к ребру (-2, 0) и (0, -2). Имеем два равных квадрата. Дальше очевидно.

Третий: сумма чисел нечетна, сразу можно сказать нет.

Четвертый: применяем операцию к ребру под ребром (1, 1). Два равных квадрата. Дальше очевидно.

Пятый: 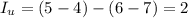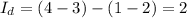$I_{u}=(5-4)-(6-7)=2$ , $I_{d}=(4-3)-(1-2)=2$ . Так что можно. Операция проста: производим действие над ребром (1, 2) 5 раз, над ребром (4, 3) один раз.