Пусть дана правильная четырехугольная пирамида SABCD.
В боковой грани проведена апофема SE.
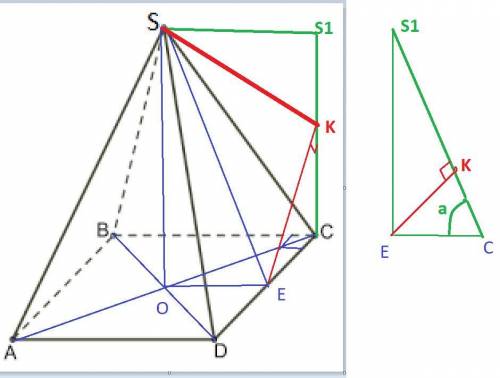
Рассмотрим проекцию SE на смежную грань BCS.
Точка S остаётся на месте, а вот точку Е надо проецировать на плоскость BCS.
Надо продлить плоскость BCS до перпендикулярной к ней плоскости, проходящей через ребро CD, в котором находится основание апофемы точка Е.
Приведен рисунок со схемой такого проецирования.
Для конкретных условий необходимы данные по пирамиде - длина ребра основания и угол наклона боковой грани к основанию.
Или же другие данные, определяющие пирамиду.
2
Пошаговое объяснение:
Предположим, что семиугольник только один. Тогда количество вершин у шестиугольников равно 40 − 7 = 33. Этого не может быть, потому что число 33 на 6 не делится.
Если семиугольников два, то количество вершин у шестиугольников равно 40 − 14 = 26, чего быть не может.
Если семиугольников три, то количество вершин у шестиугольников равно 40 − 21 = 19, чего быть не может.
Если семиугольников четыре, то количество вершин у шестиугольников равно 40 − 28 = 12. Значит, может быть 2 шестиугольника.
Больше четырёх семиугольников быть не может.
ответ: 2.
m/5= х+ 1/5
5* m/5=5х+5*1/5
m=5х+1
-(5х+1):5= -5х-1:5=-х-1